
본 포스팅은 성균관대학교 최재영 교수님의 '컴퓨터 비전(Computer Vision)' 강의 내용을 참고하여 작성되었습니다.
컴퓨터 비전 :: Stereo Vision
- 2대의 카메라 이용 → 각 카메라에서 영상을 얻어서 처리 → 객체의 깊이(원근) 파악
Two-view Geometry
· Epipolar Geometry(음극선 기하학)
: 2대의 카메라를 이용해서 각각의 Camera에서 영상을 얻어서 처리하여 객체의 깊이(원근)을 파악하는 방식이며 이를 통하여 두 이미지 사이의 관계를 구할 수 있습니다.
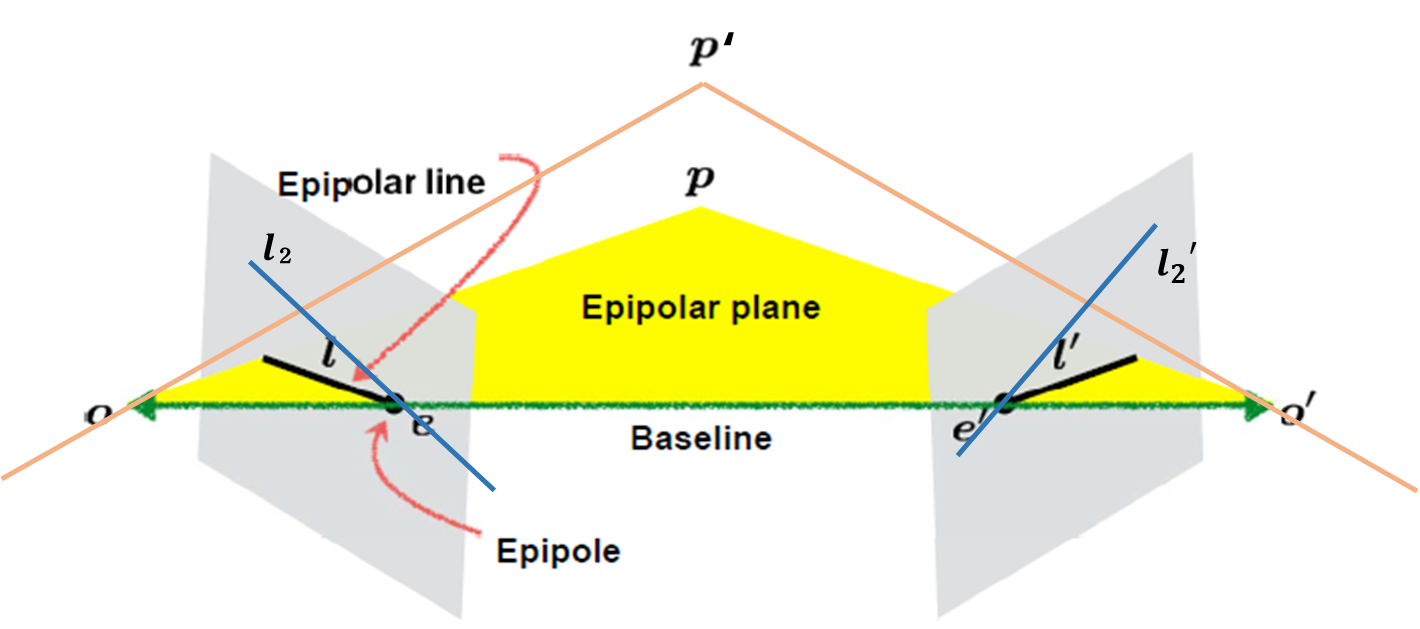
- Baseline : 두 Camera centers(O-O')를 연결한 직선
- Epiploe(e, e') : Baseline이 각 이미지에 Image에 맞닿는 점
- Epipolar line : 줄여서 epline이라고도 하며 위의 이미지에서 'ι'과 'ι''에 해당합니다. Image plane과 Camera centers(O, O')에서 초점 p와 연결한 직선이 맞닿는 점과, Epipole을 연결한 직선
- Epipolar plane : Baseline과 World point, 그리고 epipolar line을 포함하는 평면
*위 그림에서 또 다른 World point(p')에서 생성된 l_2, l_2'도 동일한 epipole(e, e')을 지난다.
*epipole은 항상 이미지 내부에 있지 않을 수도 있으며, 무한한 공간에 존재할 수도 있다.
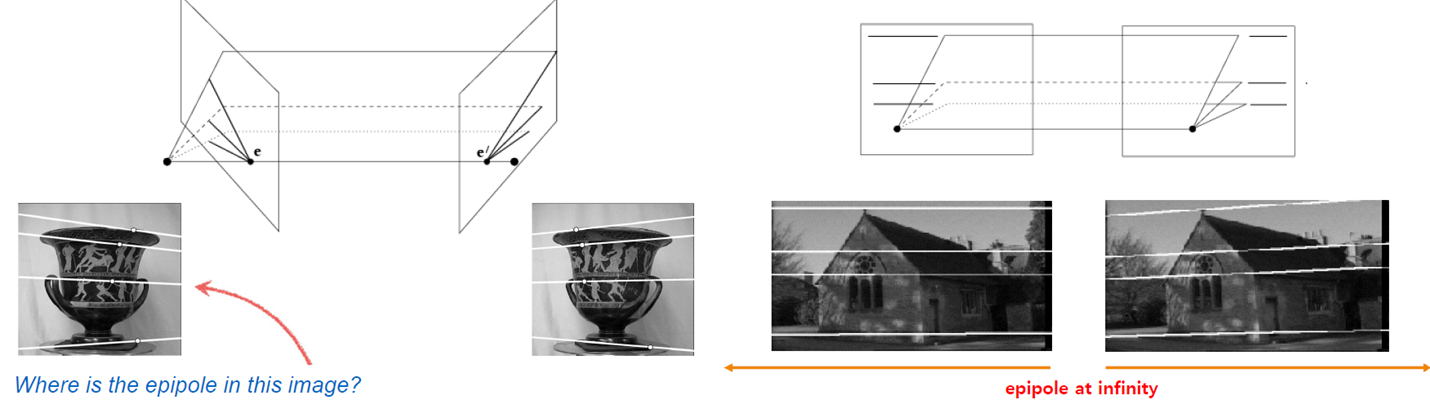
(1) Epipolar Constraint
: Epipolar line을 구하기 위해서는 두 영상간의 관계가 필요하다.

① Essential Matrix : Camera에 대한 내부적 perameter를 제거한 기본적인 내용을 가진 Matrix (*Camera는 Calibrate되었다고 가정한다)
· x가 주어졌을 때, E를 이용해서 Epipolar line을 구하는 것
· 위의 정의에 따라 Essential Matrix E를 아래의 식을 통해 구한다고 가정하자. 여기서 E의 shape는 3×3 행렬이다.
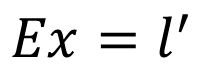
· 아래 그림에서 벡터 x와 라인 ι은 직교하므로 (x^T) × ι은 0이며 (x'^T) × ι 또한 0이다. 이는 즉 ax+by+c=0이라는 식을 생성할 수 있다.
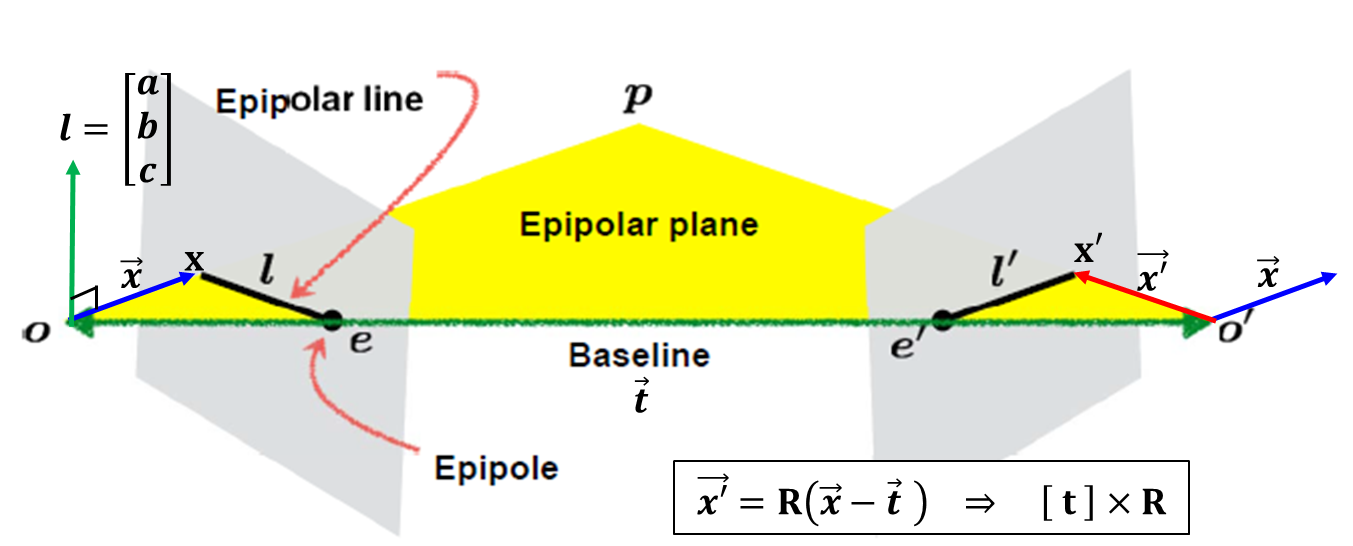
· 위의 내용을 통해 (x'^T) × ι' = 0, 그리고 E × x = ι' 이므로, 뒤의 식을 앞에 대입하면 (x^T) × E × x = 0이라는 결과를 얻을 수 있으며, 식을 정리하면 아래와 같다.

· 위의 Longuet-Higgins equation을 보면 모습이 Homography와 유사하다는 것을 알 수 있지만, Essential Matrix E는 point와 line을 연결하고, Homograpy H는 potin와 point를 연결한다는 점에서 차이가 난다.
② Fundamental Matrix : Camera의 내적 parameter까지 고려한 Matrix
· 카메라의 고유 좌표를 고려하기 때문에 전역좌표계가 아닌 픽셀좌표계로 변형된다.
· 만약 카메라의 정보가 고정된 이미지를 사용하고 있고, 초점거리로 나누어진 지점도 서로 정교하여 같다면 F=E라고 가정할 수 있다.

· 위의 식을 통해 Image정보가 Camera에 대한 전역좌표계로 변환된 식을 사용할 수 있으며 아래와 같이 Fundamental Matrix를 유추할 수 있다.

· Essential의 경우 Camera의 좌표계에서 식을 활용해야 하지만 아래와 같이 변환함으로써 픽셀좌표계를 사용할 수 있는 이점이 생긴다.

· 아래와 같이 분할하면 Fundamental matrix를 내적연산을 통해 구할 수 있다.
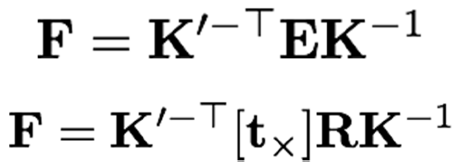
· F는 intrinsic, extrinsic parameter에 의존하는데, 아래의 식을 SVC(Singular Value Decomposition)을 통해 풀 수 있다.

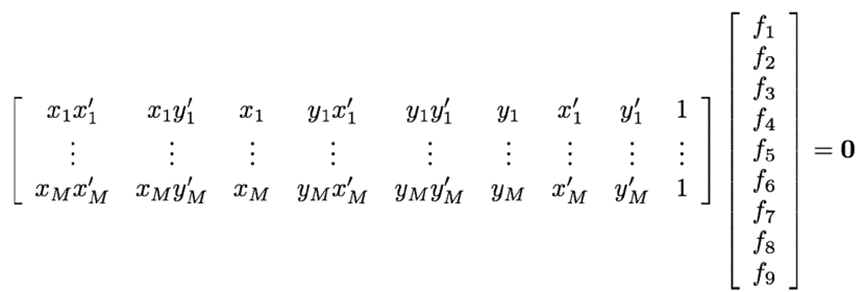
· 위 식은 9개의 unknowns를 가진 homogeneous linear system을 생성하며 이는 AX=0으로 간소화할 수 있다.
· 1개의 식이 1개의 equation만 커버하며 최소 8개의 대응점이 필요하기 때문에 Eight-point Algorithm을 활용한다.

(2) Eight-point Algorithm
① (Normalize points)
: AX = 0의 식에서 각 Column의 차이가 매우 크기 때문에, least square 계산시 오차가 많이 발생하게 되므로 이를 줄이기 위해 points를 Normalize한다. 이를 통해 points의 값이 (-1, -1)에서 (1,1)사이에 존재하도록 한다.
② Construct the M x 9 matrix A
③ Find the SVD of A
: 우측과 같이 SVD를 적용하여 A에 대한 식을 만들 수 있다. → A =U∑(V^T)
이를 통해 {f1, f2, ..., f9}를 찾아낸다.
④ Entries of F are the elements of column of V corresponding to the least singular value
: ||F-F'||이 최소값이 되는 F를 찾아낸다. 즉, Singular value를 Control하여 F'을 새로 구하여 최적화된 F를 찾는다.
⑤ (Enforce rank 2 constraint on F)
⑥ (Un-normalize F)
· ②의 M값은 대응점이 8개까지 필요없는 경우가 성립할 경우 변할 수 있다. (ex. Camera가 calibrate가 되었다고 가정)

2. Stereo Vision
(1) Triangulation

① Select point in one image
② Form epipolar line for that point in second image
③ Find matching point along line
④ Perform triangulation (삼각법 or 삼각측량법 → 깊이 계산)
: Left, Right 이미지에서 매칭된 point(x_i, x'_i)와 Camera matrices(P, P')을 통해 아래 식으로 3D Point를 예측한다.
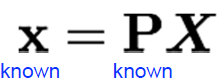
(2) Stereo Rectification
: epipolar line이 horizontal한 경우 x방향 Translation항만 살아있기 때문에 아래의 식이 성립한다.
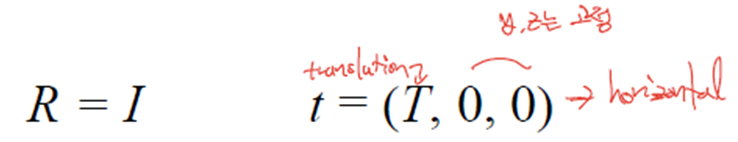
: Camera center가 같은 높이에 있으며, baseline과 focal length가 같다.
: 각 이미지는 서로 평행하며 baseline과도 평행하다.
: 식을 정리해보면 아래와 같다.

· Image Rectify의 수행
① 두 영상을 하나의 좌표축으로 변환(둘 중 하나의 좌표축에 R을 이용해 맞춘다.)
→ Compute E to get R : E = [t_x]R
→ Rotate the image by R
② 두 영상을 R_rect를 통해 Rotate하여 epipole을 무한대로 보낸다.
③ Scale을 보정한다(Focal length가 같게 조정)
· Stereo Rectification Algorithm
① Estimate E
② Estimate the epipole e(SVD of E)
③ Build R_rect from e → infinity setting
④ Decompose E into R and T
⑤ Set R_1 = R_rect, R_2 = R×R_rect
⑥ Rotate each left camera point(warp image)
[x' y' z'] = R_1[x y z] → Homography와 유사 X' = HX, H=kR_1 (*k는 camera 정보)
⑦ Rectified points as P=f/z' [x' y' z']
⑧ Repeat (6) and (7) for right camera points using R_2
+ scaling(focal length가 같도록)
(3) Depth Estimation via stereo matching
- 멀면 멀 수록 이미지 변화 차이가 적고, 가까울 수록 큰 변화를 이용
- 이미지에서 모든 epiline을 구한다면 전체 영상의 깊이를 예측할 수 있다.
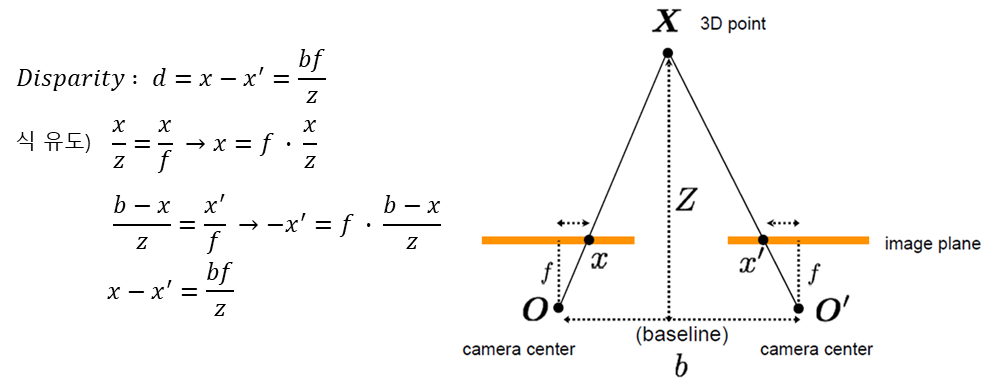
(카메라와의 거리는 수평적 차이와 반비례)
- Stereopsis : 두 눈을 사용함으로써 깊이를 판별 (오른쪽 눈과 왼쪽 눈이 바라보는 각도는 다르다) → Disparity

· (Basic) Stereo Matching Algorithm

- 변수 : Window size(패치), 영상의 특성(texture, occlusion, 같은 패턴)에 영향을 많이 받는다.
- 위 그림에서 disparity = x_2 - x_1
- 대응하는 점을 찾는 방법
① Zero mean : mask filter를 사용하여 평균값을 빼준 후 정규화
② SSD : Sum of squared diff'
③ NCC : Normalized cross-correlation
· Disparity Space Image(DSI)
- 두 영상을 비교해가며 각각 발생한 차이점들을 하나의 Matrix로 저장 → 영상화(Image)
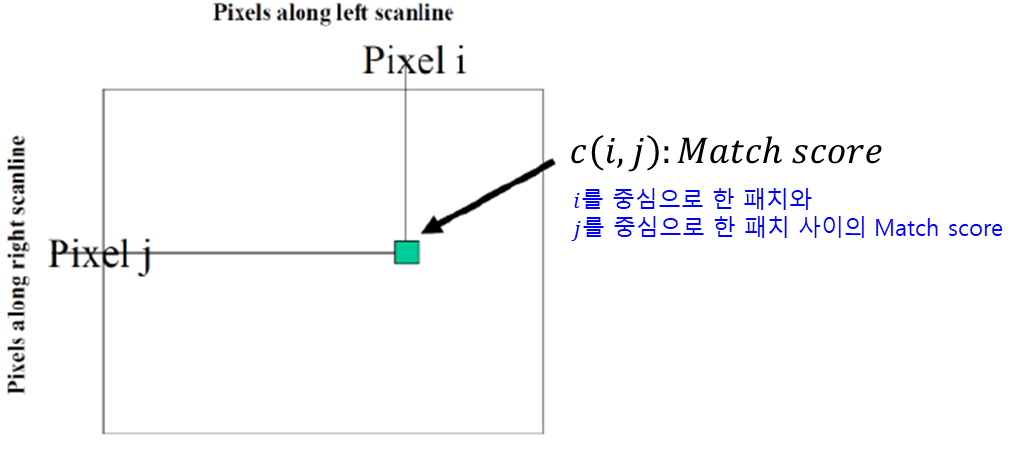
- 유사점을 epiline을 따라 Local에서 대응하며 ref와 같은 값을 찾는다.
- DSI는 row 하나당 발생(ex. 600개의 row → DSI가 600개 생성) → 추후 row간 보정도 해준다.

· Depth from Disparity
'DataScience > 컴퓨터비전' 카테고리의 다른 글
| 컴퓨터 비전 :: Feature Matching (0) | 2023.06.19 |
|---|---|
| 컴퓨터 비전 :: Feature Descriptors (1) | 2023.06.18 |
| 컴퓨터 비전 :: Local Feature Detection (1) | 2023.06.17 |
| 컴퓨터 비전 :: Image Pyramids (0) | 2023.06.16 |
| 컴퓨터 비전 :: Linear Filters(Cross-correlation, Convolution) (0) | 2023.06.15 |




댓글