
본 포스팅은 성균관대학교 최재영 교수님의 '컴퓨터 비전(Computer Vision)' 강의 내용을 참고하여 작성되었습니다.
컴퓨터 비전 :: Local Feature Detection
Local Features
· Local feature의 특징
- 이미지 매칭의 과정 : Extract features(Detection → Description)s → match features → align image
- Local feature의 이점
① Locality(지역적 특성) : Robust to occlusion and clutter
② Quantity : 하나의 이미지에서 수많은 특징을 찾아낼 수 있다. → 효율 측면에서 필요한 몇 개만 추출
③ Distinctiveness(구분성, 독창성) : 다른 특징들과 구분될 수 있다.
④ Efficiency (효율성) : (전체가 아닌) 지역적 특성을 찾기 때문에 실시간 수행 가능
· Local feature detection의 종류
(1) Point detection
① Edge detection : 미분으로 값의 기울기 변화량 확인(Prewitt, Sobel, Robert)
② Line detection : 파편화 되어있는 Edge들의 연결(Canny, Hough)
(2) Region detection
① Corner detection : Line과 Line이 만나는 부분
③ Blob detection : Characteristic region, Laplacian of Gaussian
Edge detection
- Continuous한 Image를 미분 → Kernel 이용하여 Discrete하게 변환한다.
(1) x성분에 대해 미분 : 수직적 Edge 성분 발견
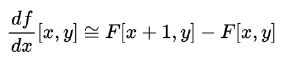
(2) y성분에 대해 미분 : 수평적 Edge 성분 발견
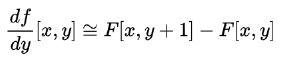
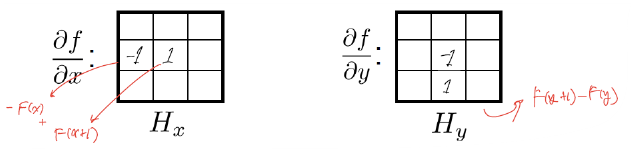
· Image Gradient

- Edge strength (=gradient magnitude)

- Gradient direction
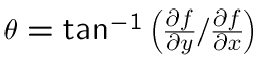
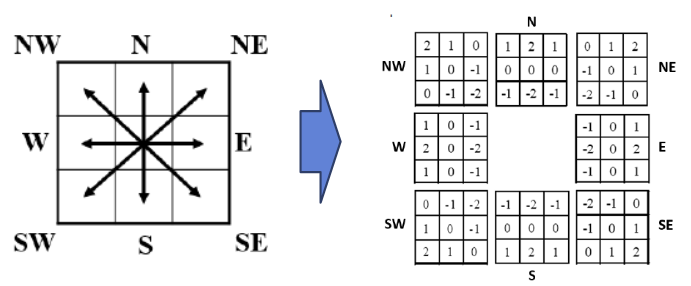
· Compass Gradient mask
- mask를 통한 계산값이 가장 큰 차이가 나는 곳을 선택하여 그 기울기를 취한다 → Maximum response
· Edge Detection의 순서
① Filtering : noise 제거(Smoothing, Blurring)
*Trade-off가 있음 : Filtering을 너무 강하게 하면 Edge가 약해진다.
② Enhancement : 중요한 변화부분 강조
③ Detection : Edge 찾기
· Edge Detection의 종류
(1) Prewitt Operator
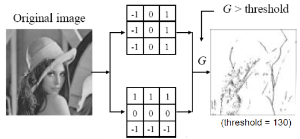
(2) Sobel Operator

(3) Robert's cross Operator

Line detection
- Three major issues in edge detection
(1) Scale이 다른 경우 선택되는 Interpolation에 따라 magnitude가 바뀌고 이에 따라 선택하는 값이 서로 다를 수 있음
(2) Gradient magnitude가 두꺼운 부분은 어떻게 처리해야 하는가
(3) Edge를 어떻게 연결해야 하는가
· Canny Edge detector
(1) DoG(Difference of Gaussians) : noise 제거 후 미분
(2) Gradient의 크기와 방향을 찾는다.(Scale filtering)
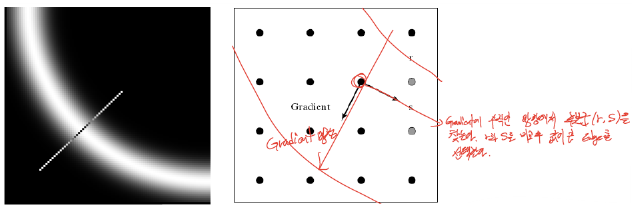
(3) NMS(Non-maximum suppression)
: Gradient에서 수직인 방향에서 후보군(p, q, r)을 찾고 높은 값 하나만 채택한다.
(4) Linking and Thresholding(Hysteresis)
: NMS를 썼을 때 굵은 Edge가 얇게 정리되지만, 일부 구간에서 끊김현상이 발생하는데 이를 해결하는 방법이다.
① Gradient값이 충분히 큰 값인지 확인
② Threshold를 2개 선정
(High threshold에 해당되는 값이 끝나는 부분에 Low-High구간 threshold에 속하는 값이 있는지 확인 후 연결해나가는 방법)

· Hough Transform
- Image에서 찾은 Edge정보를 활용하여 Line, Curve, Circle등을 찾는다.(방정식을 이용)
① 점좌표 [a, b] 이용 : Edge를 찾은 후 Line 연결(y=ax+b)
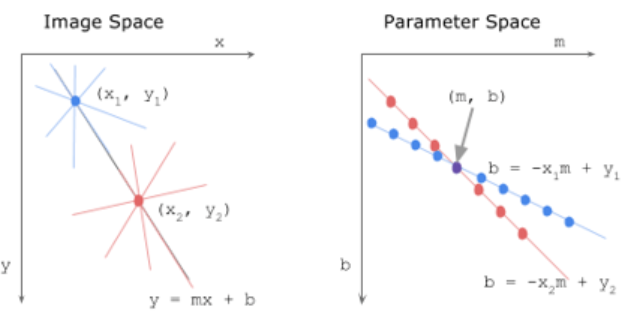
② 극좌표 [ρ, θ] 이용
: 점좌표와 달리 배열의 크기를 직접 지정할 필요 없음(계산시 자동으로 배열 생성해서 계산됨) → 범위가 명확
: 기울기가 무한대가 되는 경우를 회피
: The polar representation of straight line
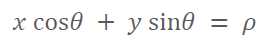

Corner detection

· Finding Corners
① 점들의 변화값 계산
② ①의 변화값들을 matrix화(H matrix : 2nd moment matrix)

③ Eigen Vector와 Eigen Value 계산
④ Threshold를 초과하는 Eigen Value를 갖는 점 → Corner
· Harris Corner Detection
: SSD(Summing up the squared differences)
: Error가 높으면 "Corner"를 찾는다.

→ Taylor Series Expansion of I
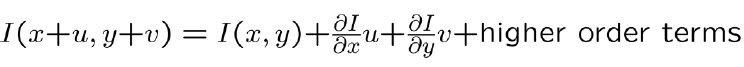
*u, v가 매우 작다면
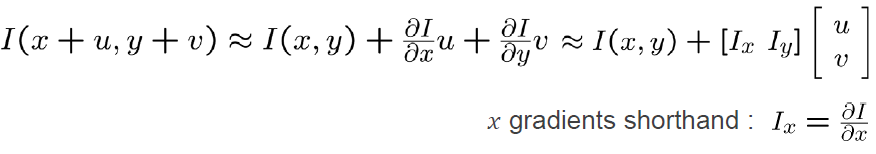

- SSD Error

위 식은 아래와 같이 풀이할 수 있다.
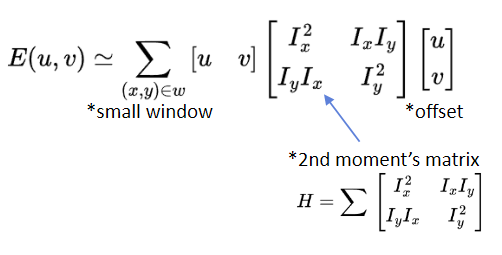
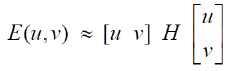

· Compute eigen vectors and eigen values
- Singular value Decomposition(SVD)
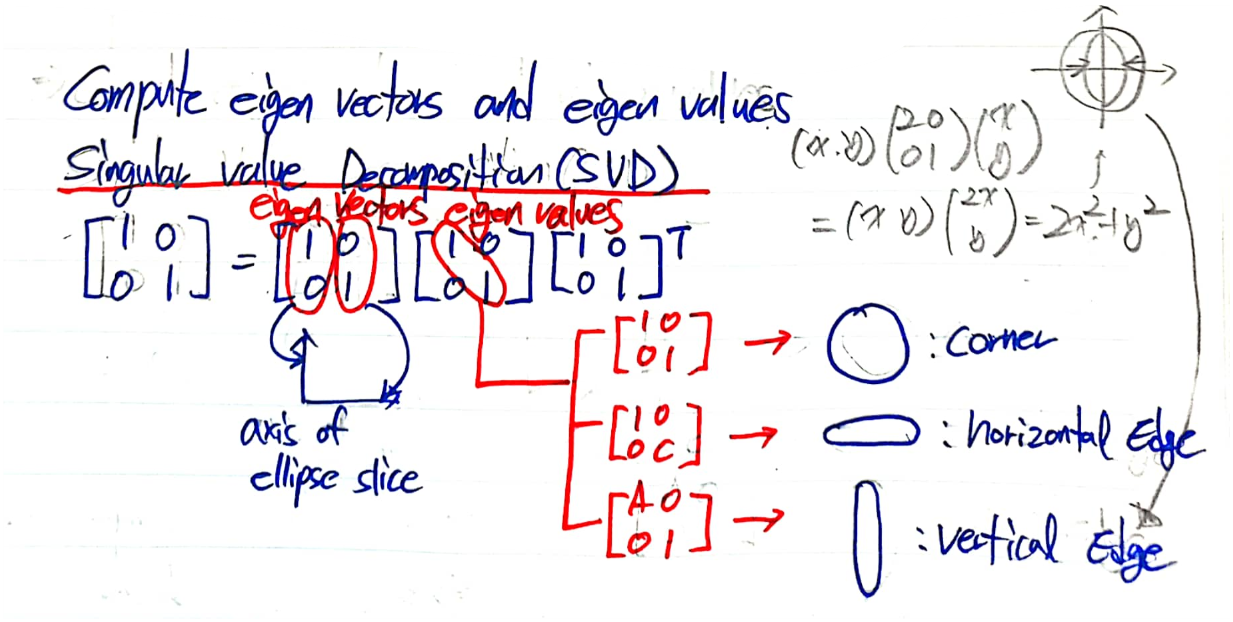
→ Ae = λe → (A-λ)e = 0 (A : H, e : eigen vector, λ : eigen value)
→ det(A-λI)=0을 통해 λ값을 구한다.
→ 구해진 λ로 eigen vector e(=[x y]^T)를 아래 식을 통해 구한다.
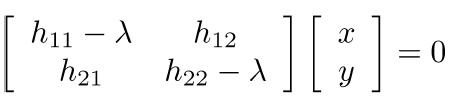
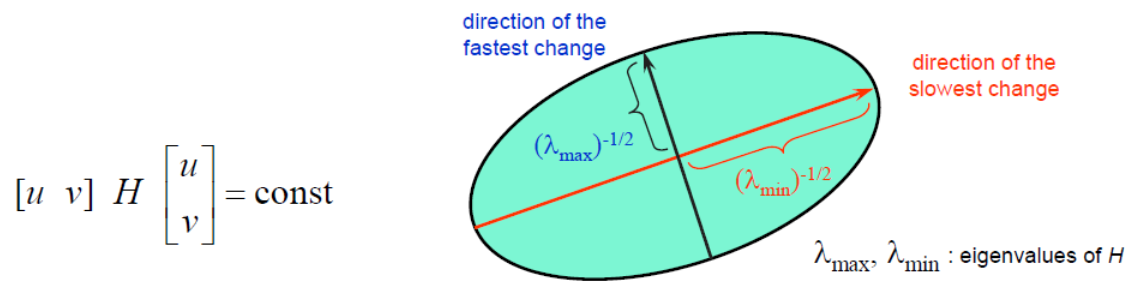
→ H는 Symmetric하기 때문에 아래처럼 표현 가능하다. (이를 통해 Edge인지 Corner인지 판별)

· Ellipse equation
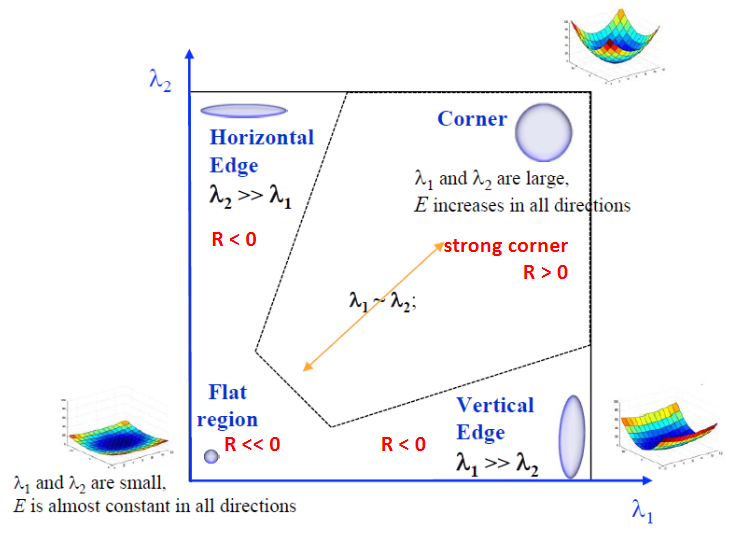
- Threshold
(1) Harris&Stephens : R = det(H) - α trace(H)²
(2) Shi&Tomasi : R = min(λ₁, λ₂)
(3) Nobel : R = det(H) / {trace(H) + ε}
· Invariance Properties : Harris detector
(1) Affine intensity change

case1) Intensity shift(I → I+b) : 전체 값의 차이가 전체적으로 상승, Corner detection에 무리 없음(Robust)
case2) Intensity scaling(I → a×I) : 같은 비율(a)의 Scaling 결과에도 특정값은 큰 변화를 보이나, 특정값에는 변화의 폭이 달라 detection 결과가 달라질 수 있다.

▶ Harris detector는 Affine intensity에 대해서는 부분적으로 불변(Partially invariant)하다
: Intensity shift에는 Robust, Intensity scaling에는 Weak
(2) Translation, Rotation
case1) Translation : Harris detector는 Translation에 대해서 공변(Covariant)한다
case2) Rotation : Harris detector는 Rotation에 대해서 공변(Covariant)한다
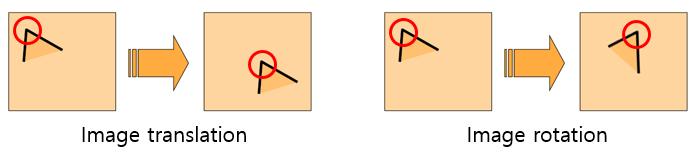
(3) Image scaling
case1) Scaling : Harris detector는 Scaling에 대해서 불변하지 않다.(Not invariant)

▶ 이를 해결하기 위해서는 윈도우 사이즈를 키우기 보다는 같은 윈도우 사이즈를 갖고 영상의 사이즈를 줄여가면서 코너를 찾는 것이 유리하다.
※ Harris Detector's Invariance property
| Affine intensity change | Translation & Rotation | Scaling |
| partially invariant Intensity shift → Robust Intensity scaling → Weak |
Covariant | Not invariant |
· Invariance vs Covariance
(1) Covariant → features(transform(image)) = transform(features(image))
▶ 영상에 변화를 가해도 이미지의 특징은 불변(Robust) 하다
(2) Invariant → features(transform(image)) = features(image)
▶ 영상에 변화를 주고 특징을 찾아낸 것과, 영상의 특징에 변화를 준 결과는 동일하다.
Blob detection
· Laplacian of Gaussian : Harris detector
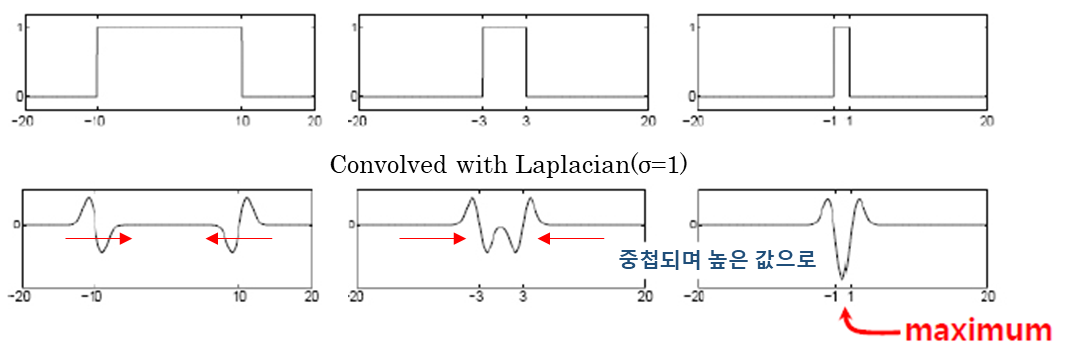
(1) Affine intensity change : Blob과 유사한 형태이기 때문에 Blob을 찾는 데 유리하다.
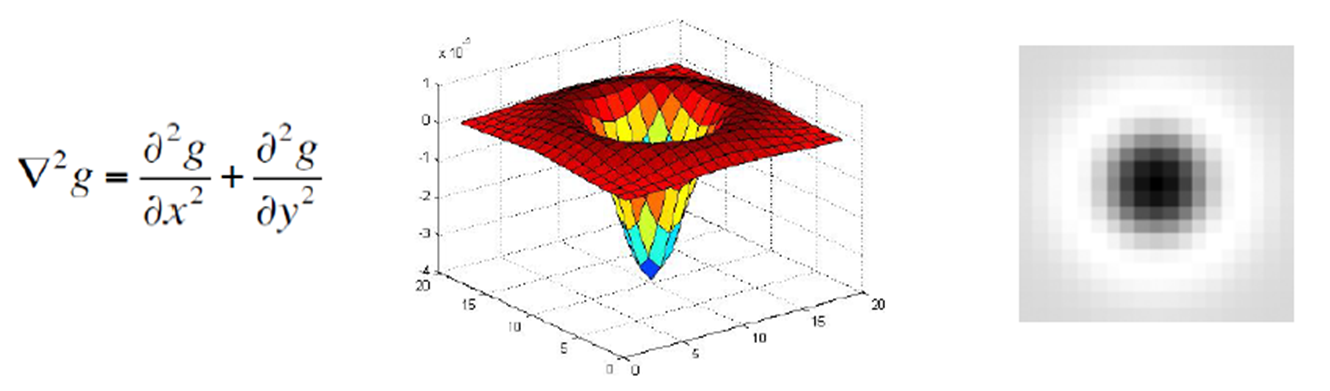
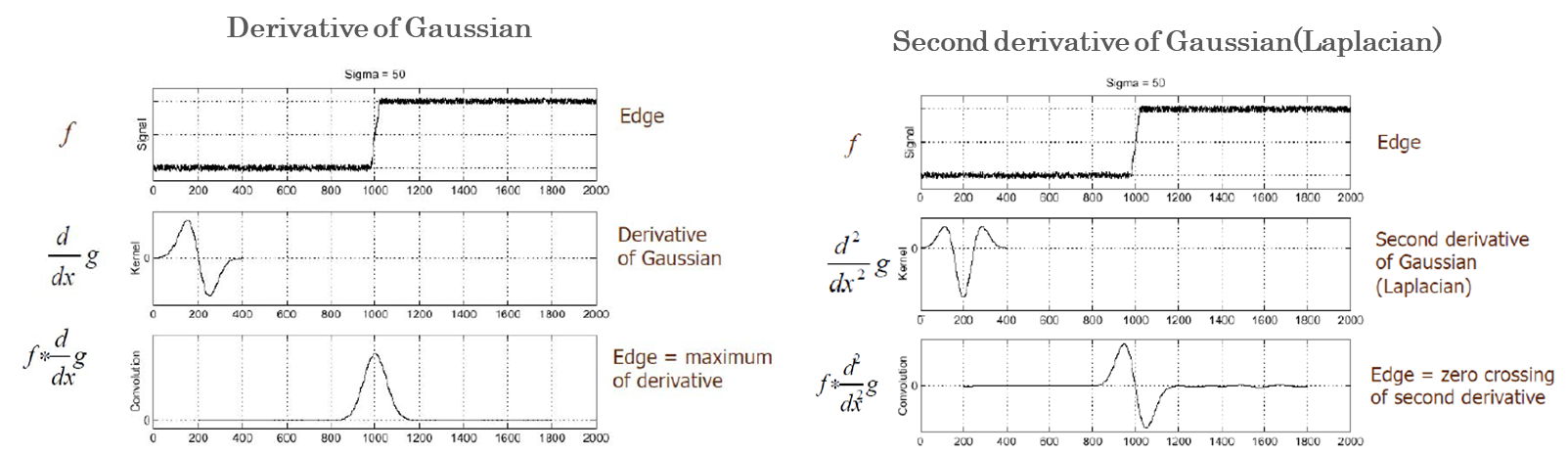
- 아래의 그림을 보면 Laplacian이 3번째 그림에서 값이 중첩되어 σ=1 반경의 Blob을 가장 잘 찾게 된다.
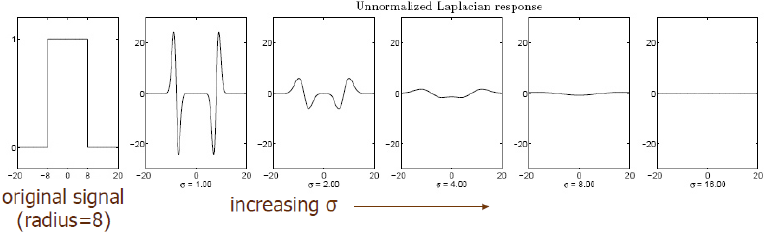
· Scale Normalization/Selection
- Unnormalized Laplacian response에서는 반경 σ이 커질수록 응답시그널의 크기가 점점 작아진다.
- Scale normalization
: σ가 커질수록 면적(1/{σ√(2π)})이 작아진다(=응답 시그널의 크기가 작아진다.)
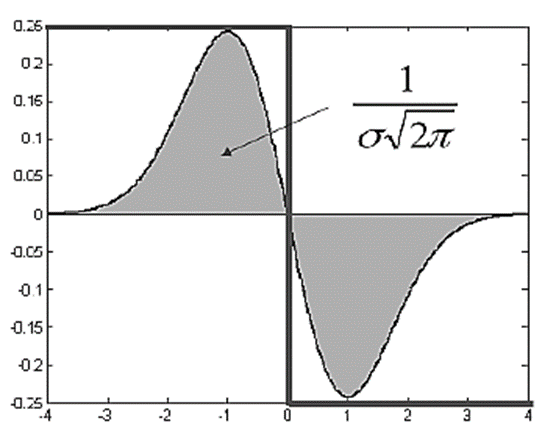
→ Normalization : Gaussian derivative에 σ를 곱한다.(Laplacian은 2차미분이기 때문에 σ²를 곱한다.)
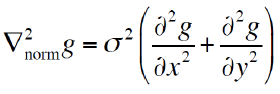
- Scale selection : 최적의 Scale을 찾는 것.
Laplacian 식을 풀어보면 아래와 같다.

위 식에서 r² - 2σ²이 0이 될 때 최적인 scale을 찾을 수 있다. 즉 아래 식을 통해 가장 최적화된 반경(=σ)을 찾을 수 있다.

· Efficient implementation
- 연산에는 Laplacian보다 DoG(Difference of Gaussians)을 이용하는 것이 연산에 효율적이다.
- 실제로 Laplacian과 DoG는 Signal 형태가 아래와 같이 유사하다.
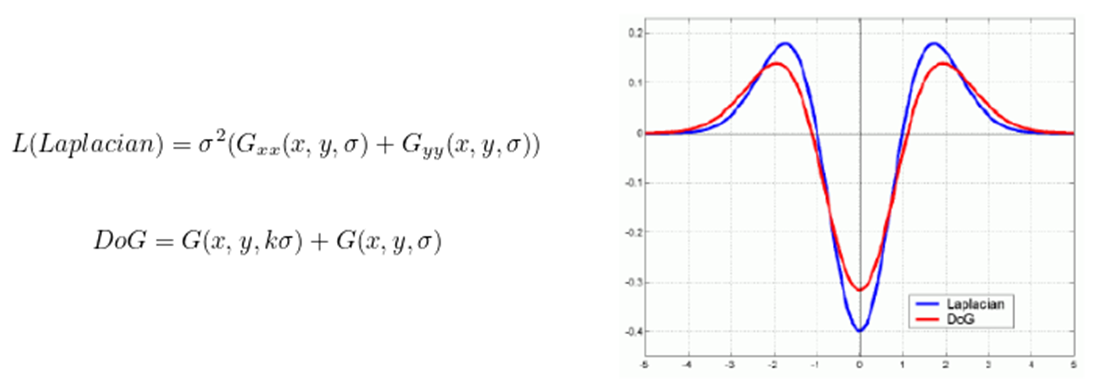
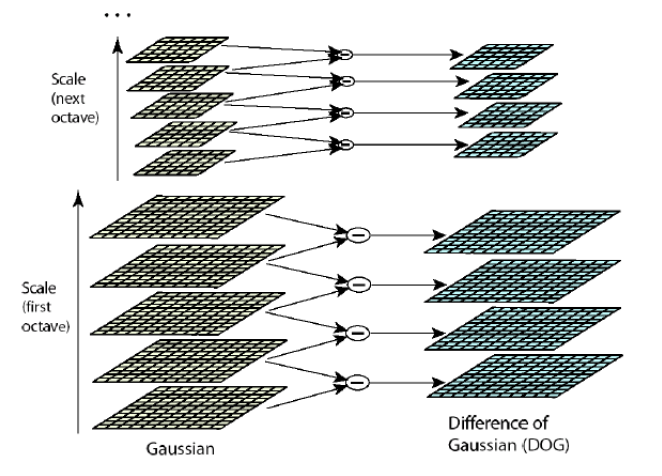
*Octave : 일정한 스케일별로 하나의 영상 크기에 적용
- Blob location and scale is covariant w.r.t. rotation and scaling
- Laplacian (blob) response is invariant w.r.t. rotation and scaling
- CNN에서는 위의 두 가지 형태를 모두 사용한다.
: Convolution Filter 사용시 shape, edge, texture에 대한 특징은 Covariant하고, 차원을 축소하면서 Invariant(bias없이 robust)하게 만든다.
'DataScience > 컴퓨터비전' 카테고리의 다른 글
| 컴퓨터 비전 :: Feature Matching (0) | 2023.06.19 |
|---|---|
| 컴퓨터 비전 :: Feature Descriptors (1) | 2023.06.18 |
| 컴퓨터 비전 :: Image Pyramids (0) | 2023.06.16 |
| 컴퓨터 비전 :: Linear Filters(Cross-correlation, Convolution) (0) | 2023.06.15 |
| 컴퓨터 비전 :: Geometric Camera Models (0) | 2023.06.14 |




댓글