
본 포스팅은 성균관대학교 최재영 교수님의 '컴퓨터 비전(Computer Vision)' 강의 내용을 참고하여 작성되었습니다.
컴퓨터 비전 :: Linear Filters(Cross-correlation, Convolution)
- 이미지에는 노이즈가 있다.(Sensor 품질, 빛의 파동, 양자화 등)
→ 노이즈를 어떻게 줄일지, 어떻게 유용한 Feature를 찾을 지
- Image Warping은 화소의 위치 변경
- Image Filtering은 화소의 값을 변경
① 이미지로부터 유용한 정보를 얻을 때
② 영상의 속성(노이즈 제거, 해상도, 훼손 복원) 향상 및 수정할 때
*CNN(Convolutional Neural Network)이란?
: 컴퓨터가 이미지의 특징을 모아 뉴런에서 내용을 인식, Local 특징들을 모아 Global Feature로 연결하는 구조
Image Filtering(Cross-Correlation)
· Point Processing vs Filter
(1) Point Processing
_하나의 포인트 연산
_사이즈, 위치, 구조변화가 없음
_Sharpening, Smoothing이 어려움
(2) Filter(=kernel)
_주변 픽셀과 함께 연산
_Sharpening, Smoothing이 가능(화소의 intensitied)
· Cross-Correlation Calculation
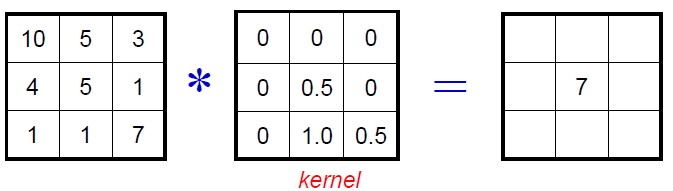
- 커널이 Stride하면서 연산하며, 연산된 화소값은 해당 위치에 전달한다.(Shift Invariant)
ex) 아래 그림에서 계산결과는 커널과 각 픽셀의 대응점을 곱하여 5×0.5 + 1×1.0 + 7×0.5 = 7의 결과를 얻을 수 있다.
- 앞의 과정을 식으로 나타내면 아래와 같다.
(f : input image, g : output image, h : kernel(2k+1×2k+1))
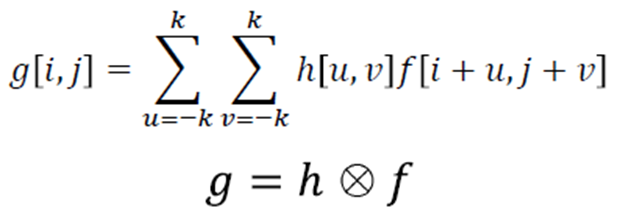
- Square mean filter → Blurring 효과(평균값)
- 통상적으로 커널의 모든 원소의 합은 1로 만든다.
(아닐 경우 영상 값이 point operation처럼 특정값으로 shift되는 현상 발생)

· Padding
- 필터 연산을 마치면 Output image의 가장자리에 나오지 않는 값들이 있는데 이부분을 Pad라고 한다.
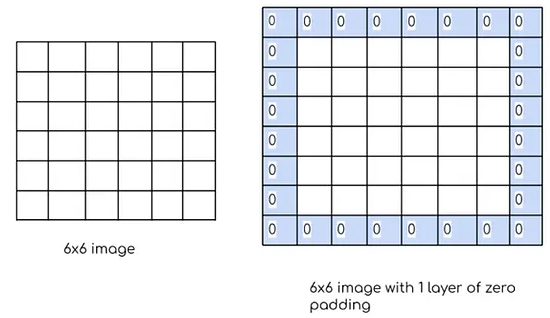
- size of the output
• Full : output size is sum of sizes of f and h
• Same : output size is same as f ⇒ “pad” is needed
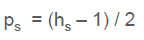
• Valid : output size is difference of sizes of f and h
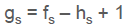
Linear Filter's key properties
(1) Linearity(선형성) : 필터를 조합해서 영상에 적용시킨 것과 각각 필터를 적용 후 합친 값은 같다.
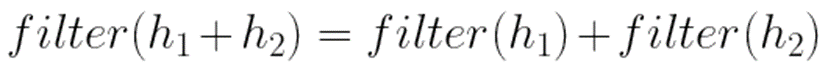
(2) Shift Invariance : 어떤 필터를 쓰든 위치변화 발생하지 않으며, Convolution으로 연산 가능하다.

(3) 필터의 조합

Gaussian Filter
· Mask가 클 경우의 특성
- 주변 화소를 더 수용. 작은 noise는 줄고, 큰 noise는 분산된다.
- 더 Blurred되며, 연산량이 증가한다.
- Blur 처리했을 때 격자모양이 생기는 문제가 여전히 남아있다.
→ 원형의 필터를 적용하면 어떨까? (Gaussian Filter)
· Gaussian Filter
- 아래 식에 의하여 가우시안 필터는 가운데 픽셀에 weight를 높게 하며, 표준편차는 smoothing 범위를 결정한다.
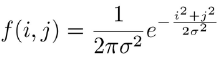

- Gaussian Filter의 장점
① 회전에 불변함
② 부드럽게 필터 적용 가능
③ σ에 따라 필터링 크기를 직관적으로 표현 가능
④ Gaussian 끼리의 연산으로 Convolution 가능
⑤ 격자모양을 개선한 Blurring 가능
- Separability
: 필터를 horizontal, vertical로 분리하여 연산이 가능 → 연산량이 감소 or 연산의 복잡도를 줄일수 있다.
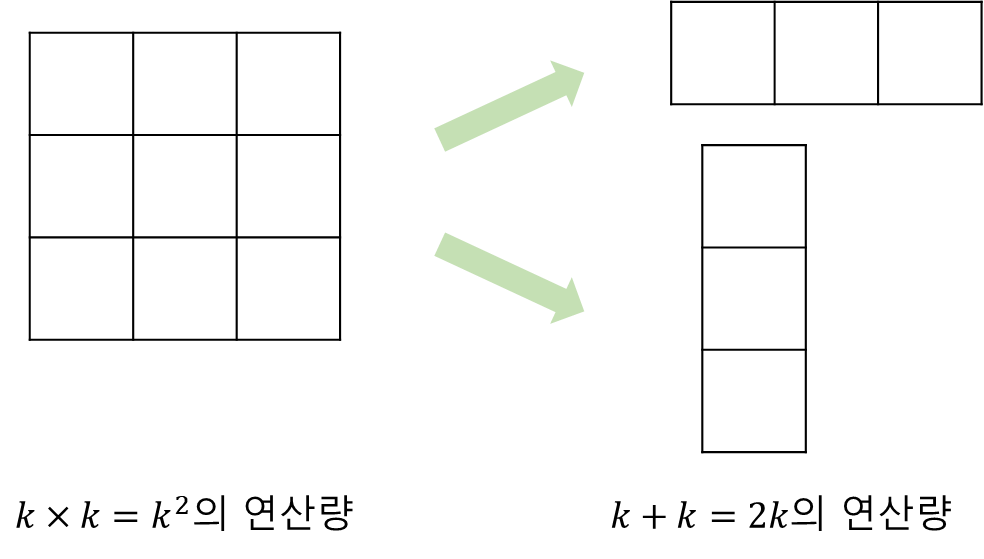
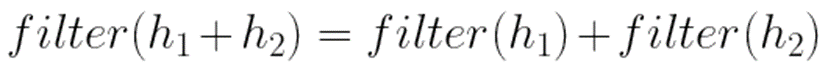
: 이를 이용하여 가우시안 필터 Fomula에 적용하면 아래와 같다.

Non-linear Filtering
- Salt and pepper noise
- Impulse noise : 국소부위 peak noise
- Gaussian noise : 가우시안 정규분포의 σ에 의해 발생하는 intensity(밝기변화에 따라 나타나는 noise)

*Replace each pixel with the MEDIAN Value of all the pixels in the neighborhood
: 주변 픽셀을 나열 후 중간에 해당하는 값으로 대체하는 방식이다. Salt and pepper noise 또는 Impulse noise의 경우 MEDIAN Value(중앙값)를 사용하면 줄일 수 있다. 이는 주변의 튀는 noise를 제거하는 데 용이하며 Mean Filter에 비해 튀는 값에 덜 민감하다. 하지만 연산에 Sorting이 포함되어 있기 때문에 연산량이 크다.
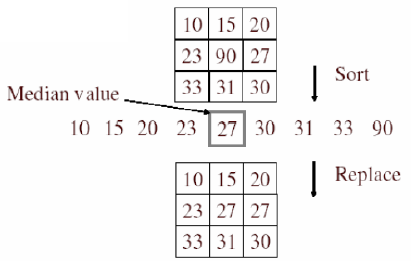
Image Filtering (Convolution)
- Convolution 연산 방법
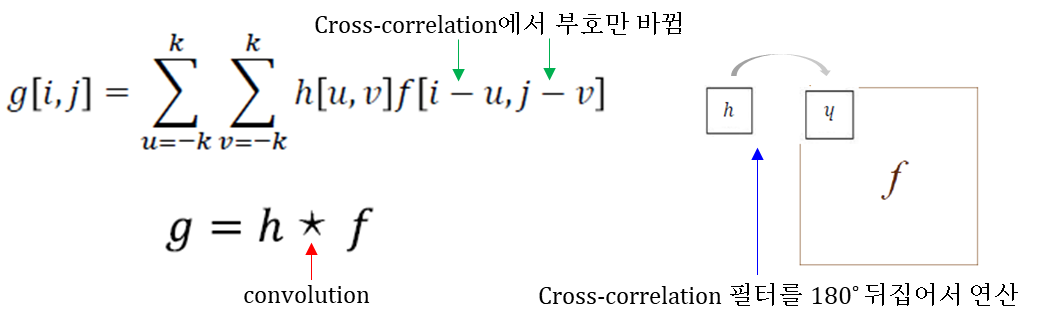
- Convolution vs Cross-Correlation
① Convolution
· 원본 이미지와 필터 사이의 두 신호의 중첩부분에 대한 면적의 합
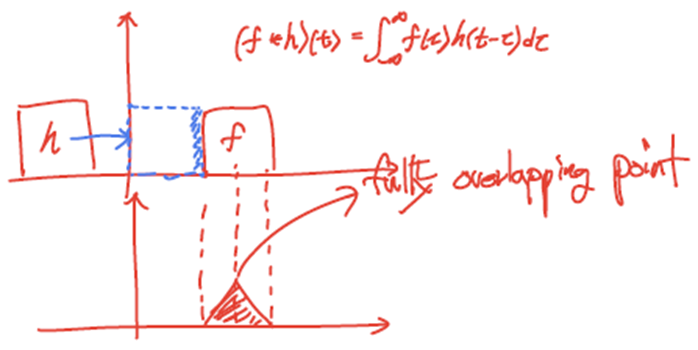
· 교환, 결합, 분배법칙, 스칼라곱, 미분에 열려있다.
· Edge detection에 유용하다.(Rapid Change in the image intensity function)

② Cross-correlation : 함수간에 유사성의 비교 척도. 값(단순 수치)으로 즉각 활용되는 변환.(원본 이미지와 필터의 두 신호가 얼마나 모양이 비슷한지)
Edge Detection
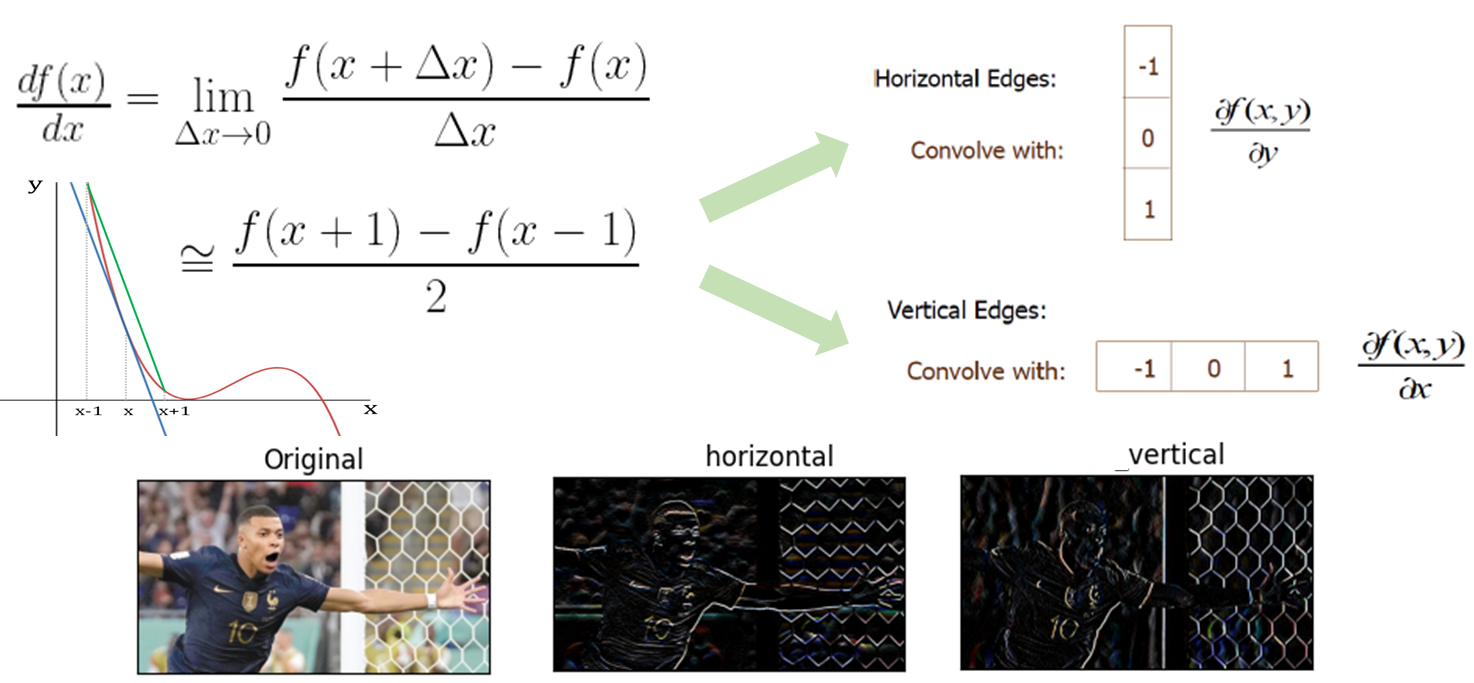
- 아래와 같이 f(x)를 미분한 식을 활용하여 Edge를 검출할 수 있는 필터를 생성할 수 있다.
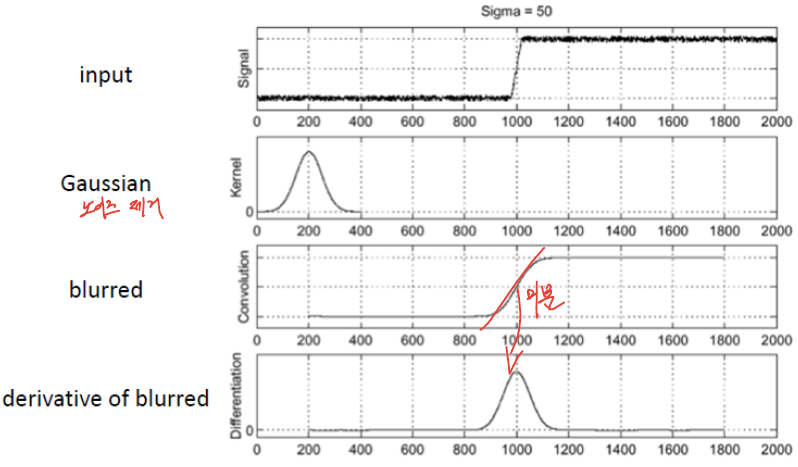
- 아래 그림과 같이 noise가 많을 경우 미분하게 되면 우측 그림과 같이 Edge를 찾기 어려워진다.

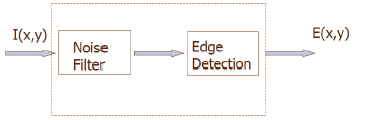
- 위와 같은 문제로 Edge Detection 이전에 Noise Filter를 적용시켜서 noise cleaning을 진행할 수 있다.
- 노이즈를 제거 및 Edge Detection을 복합적으로 동작시킬 수 있는 필터가 있다. (Prewitt, Sobel)
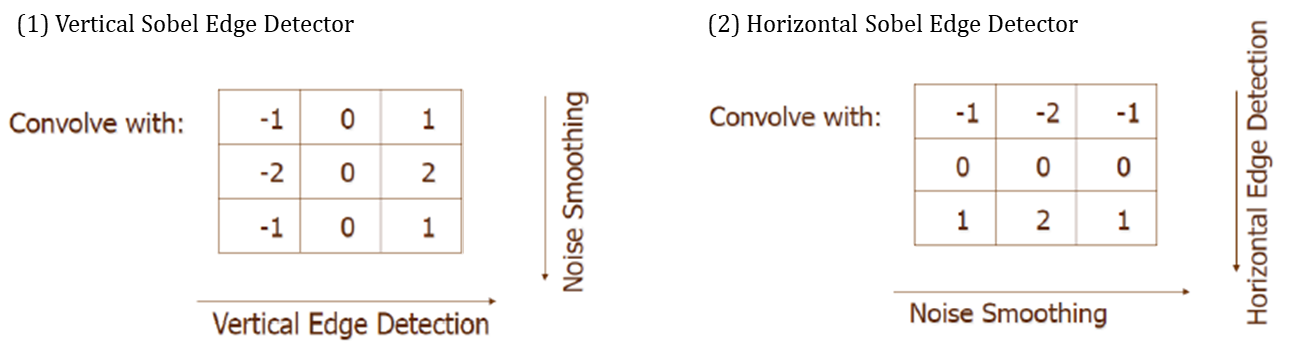
(1) Prewitt Edge Detector

(2) Sobel Edge Detector : Prewitt Edge Detector 에서 가중치를 추가하여 Edge를 더욱 도드라지게 만든다.
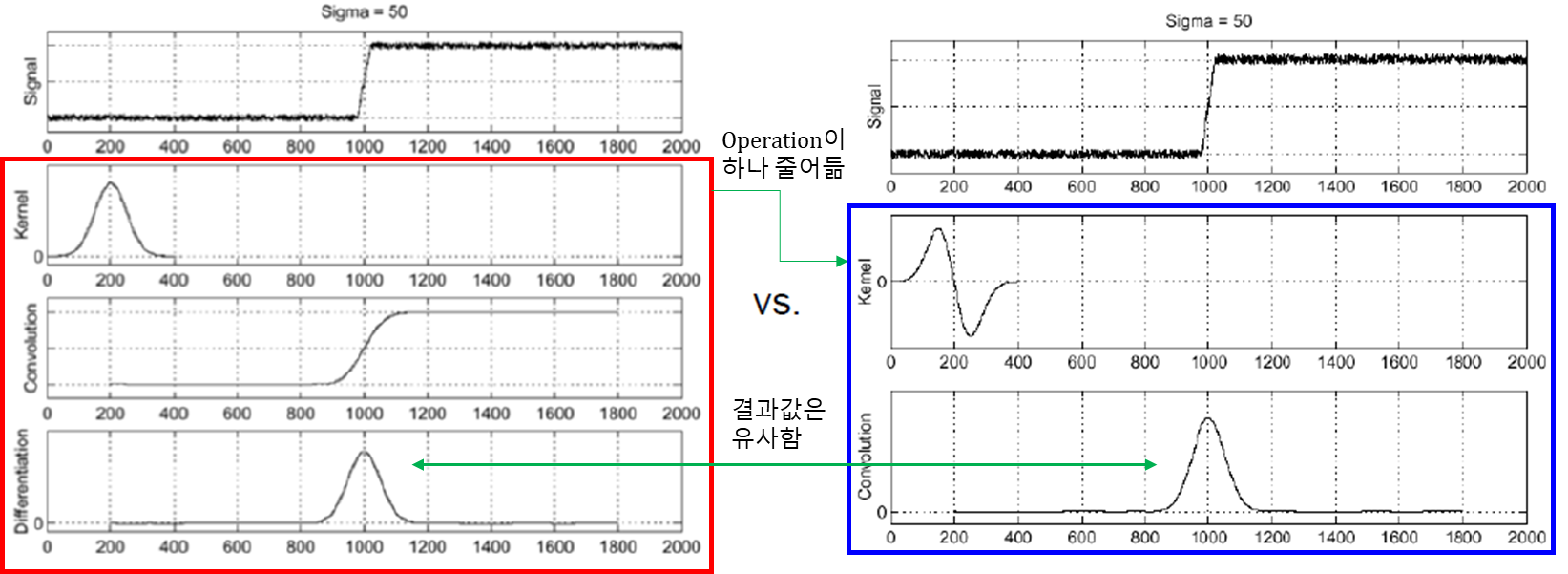
DoG(Derivative of Gaussian Filter) : 가우시안 필터 1차 미분
- 기존에는 Gaussian kernel 이후 미분 kernel이 있었다면, DoG는 가우시안 필터를 미분한 커널을 생성하여 이 커널을 통해 한번에 연산하면서 Operation을 줄일 수 있다.

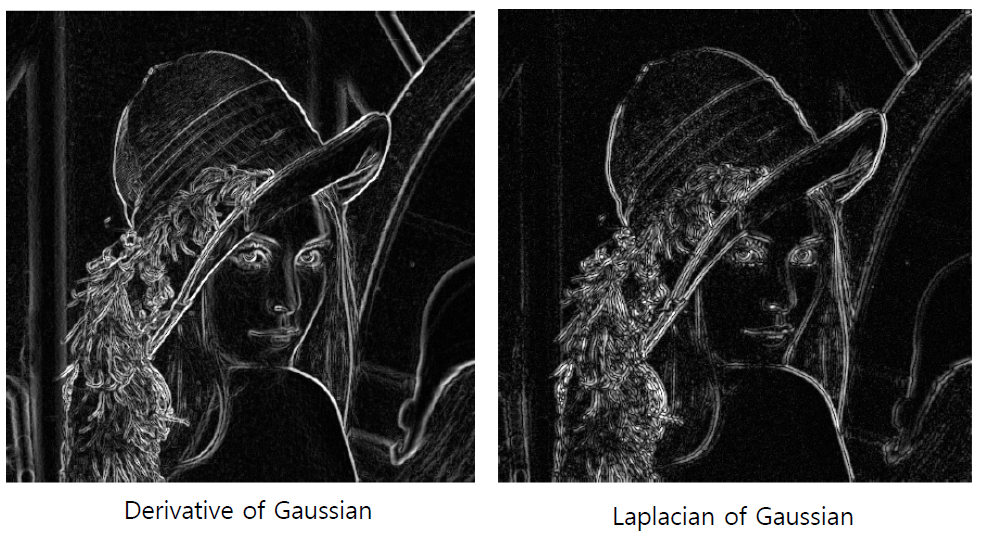
LoG(Laplacian of Gaussian) : 가우시안 필터 2차 미분
- LoG는 가우시안 필터를 2차미분하여 생성 후 적용하는 것을 말한다.
- DoG와 다르게 Zero Closing에 의해 선이 이중으로 생기는 현상이 발생하며, Non-Separable(분리 불가능)하기 때문에 연산량이 많다. 그렇기 때문에 LoG를 DoG로 Approximation하여 보통 사용한다.

'DataScience > 컴퓨터비전' 카테고리의 다른 글
| 컴퓨터 비전 :: Feature Matching (0) | 2023.06.19 |
|---|---|
| 컴퓨터 비전 :: Feature Descriptors (1) | 2023.06.18 |
| 컴퓨터 비전 :: Local Feature Detection (1) | 2023.06.17 |
| 컴퓨터 비전 :: Image Pyramids (0) | 2023.06.16 |
| 컴퓨터 비전 :: Geometric Camera Models (0) | 2023.06.14 |




댓글