
본 포스팅은 성균관대학교 최재영 교수님의 '컴퓨터 비전(Computer Vision)' 강의 내용을 참고하여 작성되었습니다.
컴퓨터 비전 :: Image Pyramids
Aliasing
· Image Down Sampling
- 해상도를 줄이는 것. Window 내 픽셀 중 하나의 값으로 대체
→ 다시 zoom in할 경우 픽셀화, 왜곡된 신호를 보여주기도 한다.
· Aliasing
- Analog 이미지를 Digital 이미지로 변환하면서 발생하는 오류 현상으로 Data 추출 interval에 다라 다른 결과를 불러오는 현상이다.
*아래 그림과 같이 Interval(=sampling rate)이 충분히 높지 않다면 추출된 point를 기준으로 영상을 표현하기 때문에 Alias(Wrong signal or image)를 발생시킬 수 있다. (ex. 왜곡, 무아레 현상, wagon-wheel현상 등)
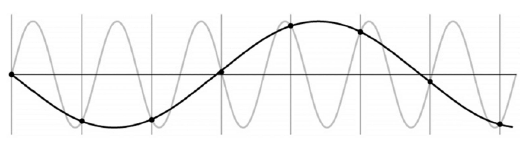
· To avoid aliasing
(1) Oversample the signal
: Nyquist rate(원신호를 복원할 수 있는 최소 주파수로 최대 주파수의 2배 이상(주기는 1/2이하))를 적용한다.
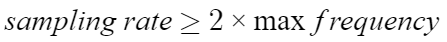
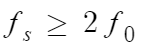
: 고주파에서 최대 주파수를 제거하는 LPF(Low pass filter)를 사용하기도 한다.
(2) Filter the image subsample
: Aliasing을 유발하는 요소를 사전에 제거 후 subsampling
: 정보 손실이 있을 수 있으나, 인위적으로 Aliasing을 하는 것보다는 좋은 효과
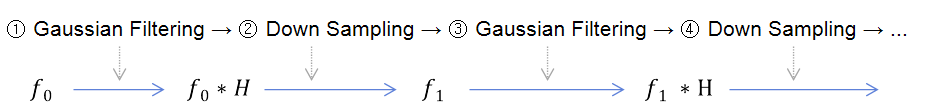
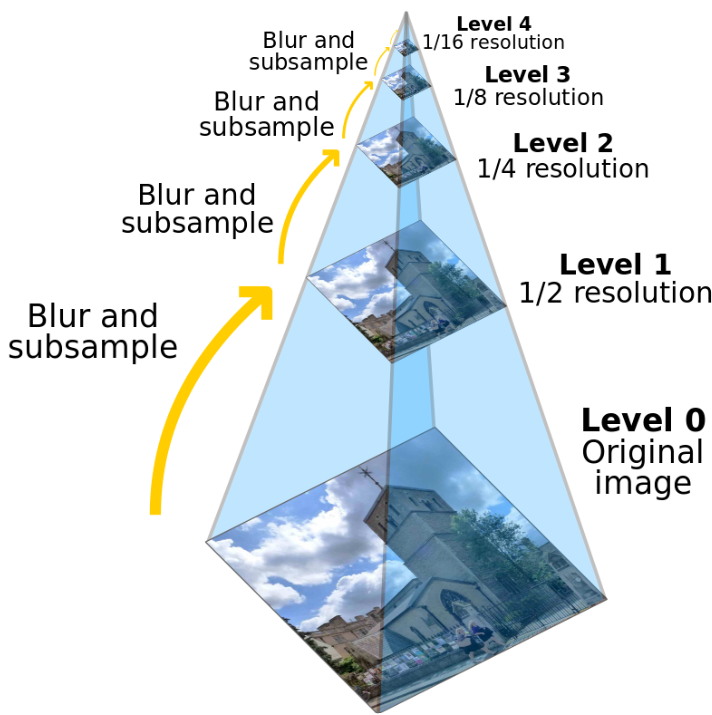
Gaussian Image Pyramid(Downsampling)
- Image를 축소, Denoising, Multiscale로 다양한 정보이해를 가능하게 한다.
- Pyramid 위로 올라갈수록 이미지가 작아지고 Smooth해진다.
→ Uniform Region에서 Global feature를 파악한다.
- Pyramid 아래쪽(큰 영상)에서는 Local feature를 찾아낸다.
- 정보손실로 원본복원은 불가하다.
- 전체 이미지의 용량 : Original * 4/3
Laplacian Image Pyramid(Upsampling)
· Multiscale decomposition

- Downsampling으로 인한 손실 : Predicted error image
- 남겨지는 정보 : 마지막 이미지 + Σ 예측 에러
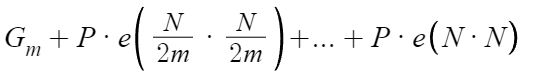
- 총 용량 = Original Image 용량
· Compute Residuals

· Reconstruction : Recover x₁ from L₁, L₂, L₃ and g₃

Gaussian Pyramid vs Laplacian Pyramid
- Gaussian pyramid : 점차 Blurred + Subsample, scale invariance
- Laplacian pyramid : Noise reduction과 Coding에 유리
· Image pyramid의 활용
- Image Compression, multi-scale texture mapping, denoising, focal stack compositing, multi-scale image analysis
Wavelet Transform
- 특수한 신호(주파수)의 집합
- 고주파, 저주파의 특성을 모두 가질 수 있으며(아래 왼쪽 그림) 시간, 공간 분해능이 뛰어나다. (아래 우측 그림)

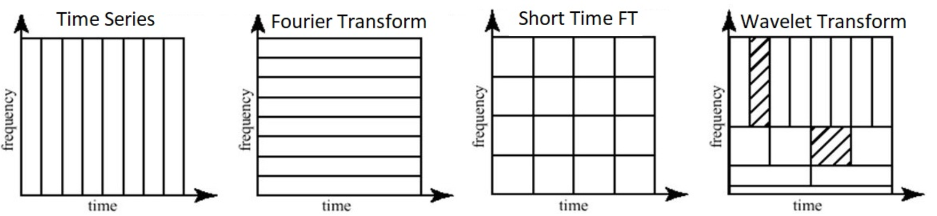
· Wavelet Transform
- 평균이 0, 빠르게 크기가 줄어드는 진동파형(Sin파는 무한 진동하나 Wavelet은 유한함)
- Scaling : 시간에 따라 신호를 늘리거나 줄이는 과정(저주파 ↔ 고주파)
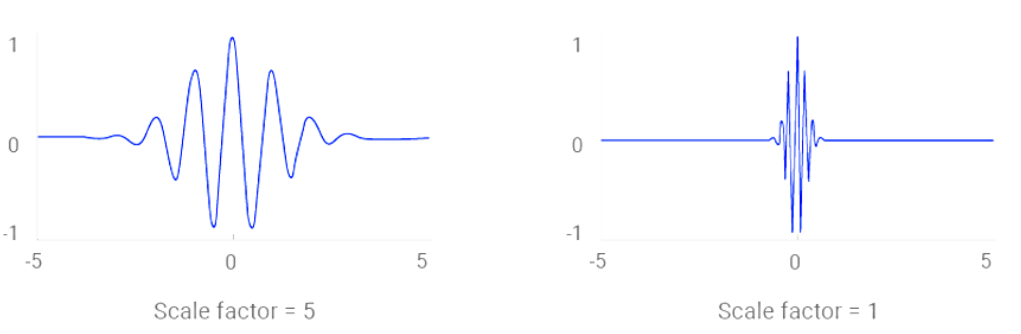

* s : 스케일링 지수(s>0, s는 주파수와 반비례)
if s > 1 → low frequency, 0 < s < 1 → high frequency
· DCT(Discrere cosine transform)의 변형
- 1D Discrete wavelet transform

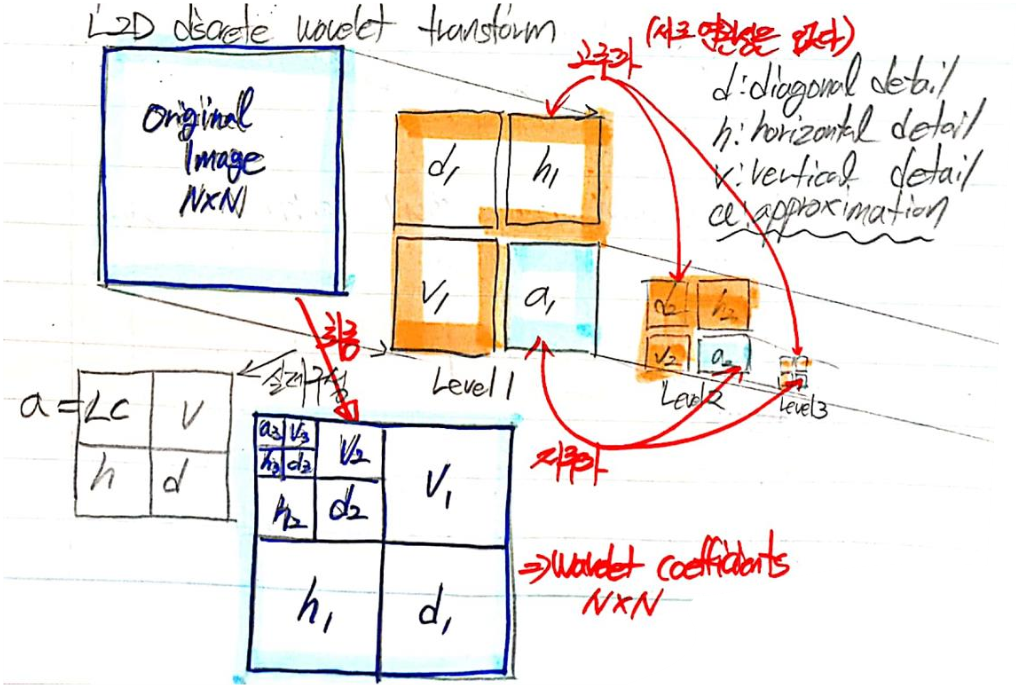
- 2D Discrete wavelet transform
Interpolation
· Image Interpolation
- Digital Image : 연속적인 포인트를 이산적으로 Point Sampling한 것

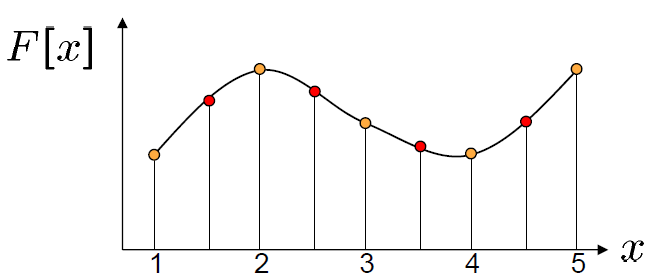
*아래 그림에서의 f(x)를 안다면 양자화 된 데이터를 쉽게 다시 원복할 수 있다.
*f(x)를 알지 못한다면? → approximation f*를 예측(Using Filtering) *아래 그림에서 h = Filtering
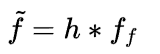
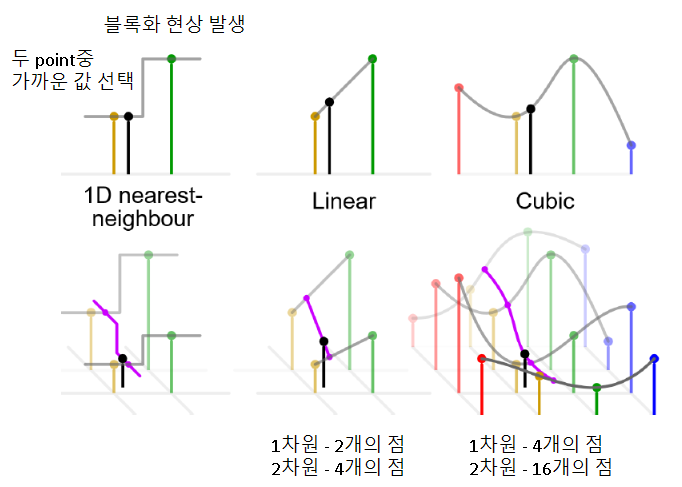
· Interpolation의 예시

· Most common Interpolation techniques
· Bilinear interpolation(x, y축)

- R₁, R₂ 대입 후 식을 정리하면 아래와 같다.
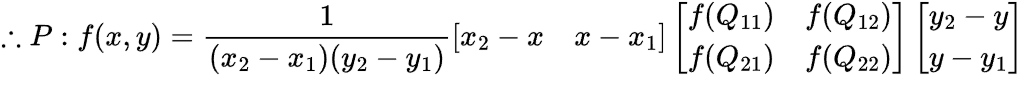
ex) 아래와 같은 matrix에서 ?에 해당하는 부분을 Interpolation한다고 하면

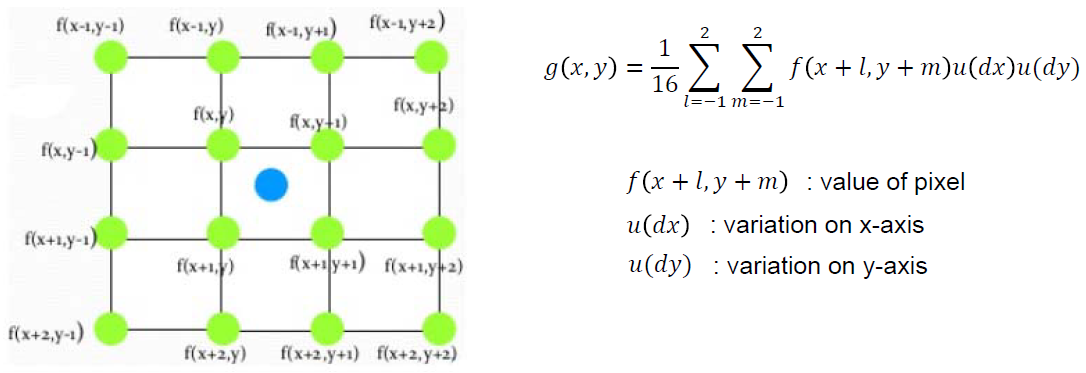
· Bicubic interpolation → 가장 부드럽게 보간
'DataScience > 컴퓨터비전' 카테고리의 다른 글
| 컴퓨터 비전 :: Feature Matching (0) | 2023.06.19 |
|---|---|
| 컴퓨터 비전 :: Feature Descriptors (1) | 2023.06.18 |
| 컴퓨터 비전 :: Local Feature Detection (1) | 2023.06.17 |
| 컴퓨터 비전 :: Linear Filters(Cross-correlation, Convolution) (0) | 2023.06.15 |
| 컴퓨터 비전 :: Geometric Camera Models (0) | 2023.06.14 |




댓글