
머신러닝 :: 9. Support Vector Machine
Support Vector Machine
· 서포트 벡터 머신(Support Vector Machine)은 주어진 데이터셋을 바탕으로 카테고리를 분류할 수 있는 선형 분류 모델을 만드는 것을 말한다.
서포트 벡터 머신(support vector machine, SVM[1][2])은 기계 학습의 분야 중 하나로 패턴 인식, 자료 분석을 위한 지도 학습 모델이며, 주로 분류와 회귀 분석을 위해 사용한다. 두 카테고리 중 어느 하나에 속한 데이터의 집합이 주어졌을 때, SVM 알고리즘은 주어진 데이터 집합을 바탕으로 하여 새로운 데이터가 어느 카테고리에 속할지 판단하는 비확률적 이진 선형 분류 모델을 만든다. 만들어진 분류 모델은 데이터가 사상된 공간에서 경계로 표현되는데 SVM 알고리즘은 그 중 가장 큰 폭을 가진 경계를 찾는 알고리즘이다. SVM은 선형 분류와 더불어 비선형 분류에서도 사용될 수 있다. 비선형 분류를 하기 위해서 주어진 데이터를 고차원 특징 공간으로 사상하는 작업이 필요한데, 이를 효율적으로 하기 위해 커널 트릭을 사용하기도 한다.
※ 출처 : 위키백과 '서포트 벡터 머신'
Linear Support Vector Machine
· LSVM의 Margin을 크게할 수록 좋은 모델이며, Support Vector는 Boundary를 기준으로 법선방향으로 이동하였을 때 처음으로 도달하는 datapoints를 Support Vectors라고 한다.
· Support Vector를 만드는 데 필요한 데이터는 '적다'. (ex. 아래 그림에서는 3개) 즉 나머지 Training examples를 무시하더라도 Support Vector만 알 수 있다면 Boundary를 그릴 수 있다.
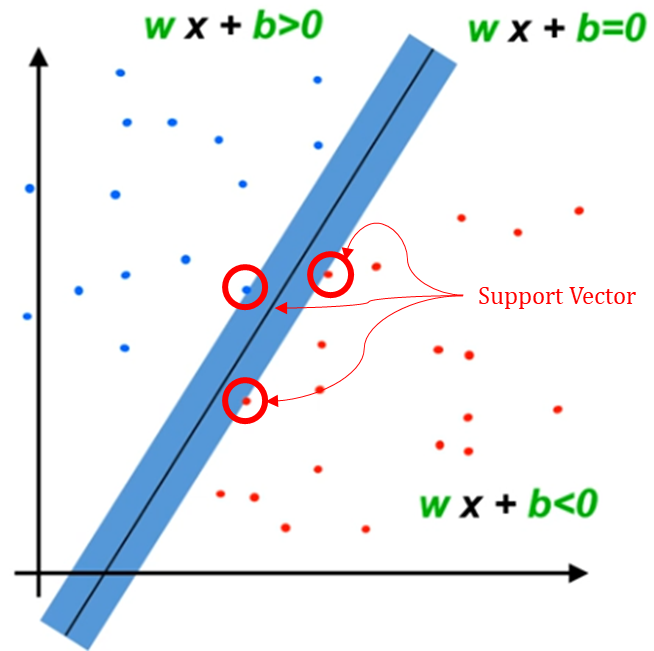
Margin
· Boundary를 기준으로 Plus Zone과 Minus Zone과의 경계까지의 거리(Distance)

· Support Vector Machine과 Margin의 특징
1) Vector W는 Boundary에 대해 직교(Perpendicular)한다. a와 b가 Boundary 위에 있는 점이라면 w(a-b)=0이 성립한다.
2) x_p Plus line에, x_m이 Minus line에 있는 점이라면, (x_p - x_m)은 Boundary에 대해 직교한다.
3) |x_p - x_m| = M (margin)
4) x_p = x_m + λW <- |x_p - x_m| = λW (λ는 상수)
* from 3), 4) ▶ |x_p - x_m| = M = λW
5) W(x_m + λW)+b = 1 <- Wx + b = 1, x = x_m + λW ---- from 4)
* from 5) ▶ Wx_m + λW·W + b = 1
6) -1 +λW·W = 1
* from 6) ▶ λ=2/W·W (*아래 식 참고)

· 위와 같이 W와 M(Margin)의 식으로 나타낼 수 있으며, W의 절대값을 작게할 수록 M이 Maximize됨을 확인할 수 있다.
· Maximize the margin M
- 아래와 같이 데이터셋이 분포되어있고, 이에 대해 Margin을 최대화하는 Boundary를 찾는다고 하자.
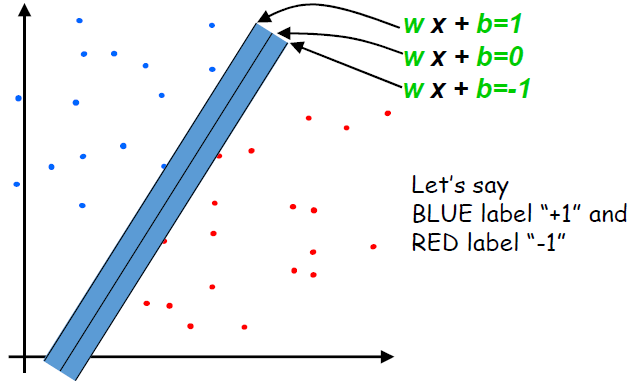
(1) All Plus points(Blue, y_i=1)are above the plus boundary
if y_i = +1, w·x_i+b >= 1 ▷ y_i(w·x_i+b) >= 1
(2) All Minus points(Red, y_i=-1)are below the minus boundary
if y_i = -1, w·x_i+b <= -1 ▷ y_i(w·x_i+b) >= 1 (1)의 식과 동일해진다.
· 결국 M을 최대화하기 위한 식을 나타내면 아래와 같다.
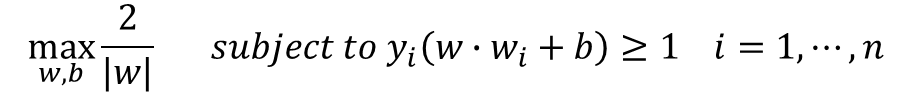
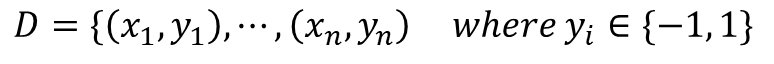
· 위의 식의 분모와 분자를 바꾸어 minimize하는 식으로 바꿀 수 있다.
→ Minimize ▷ Constraint Optimization : Quadratic programming으로 풀이한다.
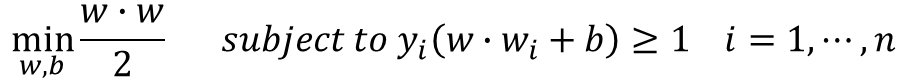
예제 1
· Given Dataset이 아래와 같을 때 maximum margin을 갖는 Boundary를 찾으려면 어떻게 해야 할까?
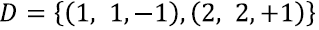
· 먼저 Quadratic programming formulation을 활용하여 아래와 같이 전개한다.

· Dataset에 있는 두 개의 Datapoints(1, 1, -1), (2, 2, 1)를 적용하면 Constraint는 아래와 같이 표현된다.
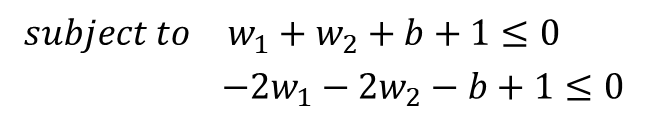
· Constraint optimization에 의해 식을 아래와 같이 전개한다.
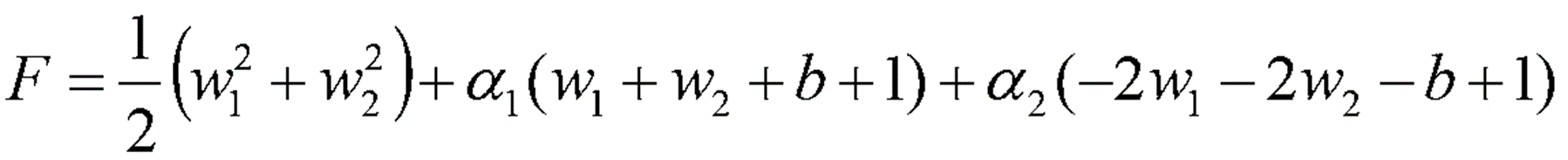
· 아래 Constraint 조건을 만족하는 W값을 Case별로 구분해서 찾는다.

· α1, α2의 조건에 따라 아래 4가지의 Case가 나올 수 있다. 하지만 아래에서 Case2, Case3은 미지수의 갯수가 식의 갯수보다 많으므로 W값을 구할 수 없다.

· Constraint 조건에 따라 아래와 같이 표현하였을 때, 마지막 두 줄의 식이 0이 된다는 것의 의미는 해당되는 두 개의 점 Datapoints(1, 1, -1), (2, 2, 1)이 'Margin 선 위에 존재.' 즉 Datapoints(1, 1, -1), (2, 2, 1)가 Support vector임을 의미한다.

Dual Form for learning LSVM
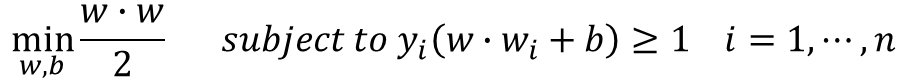
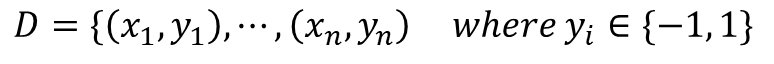
· Original Problem인 위의 식을 Lagrangian Form (+Equality/Inequality constrained condition)으로 변환하면 아래와 같다.

· 앞선 포스팅에서 언급했던 Dual Form을 활용하여 아래와 같이 max↔min 위치를 변환할 수 있다.
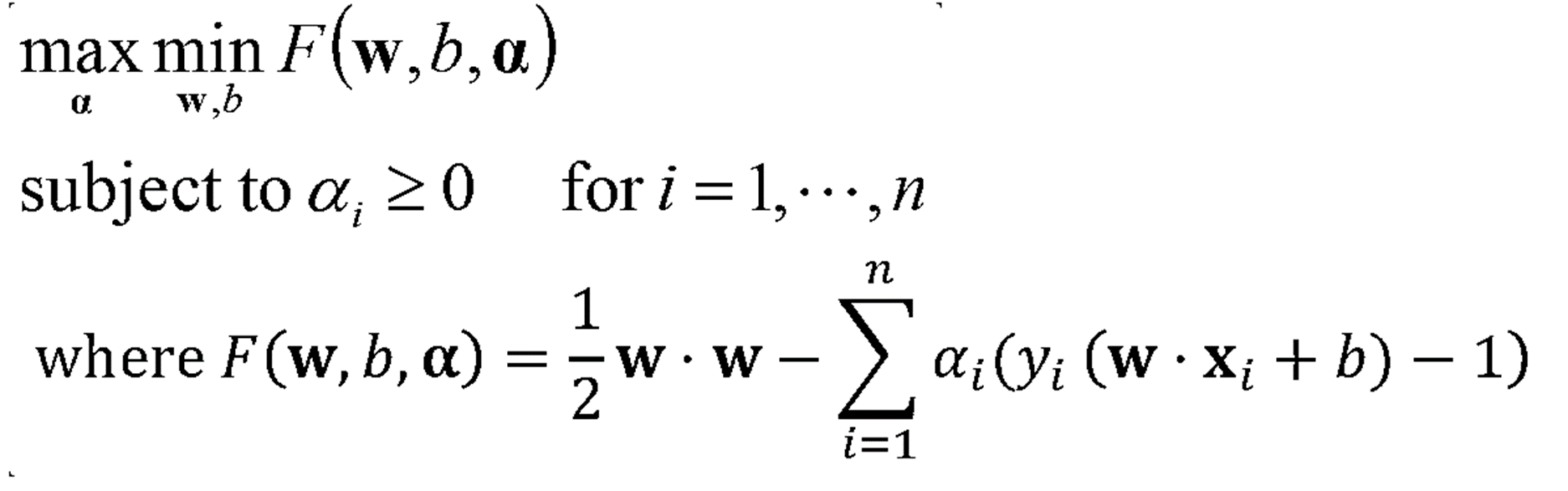
· F(w, b, α)는 Convex하다고 가정하기 때문에 위 식의 minF(w, b, α)는 조건에 따라 미분을 통해서 아래와 같이 두 개의 식을 얻을 수 있다.

· 얻어낸 두 식을 F(w, b, α)에 대입하면 minimize부분은 이제 아래와 같이 식을 변환할 수 있다.

· 위 식에서 α의 candidates{α_1, α_2, ..., α_n}들을 먼저 구한 후, 아래의 식에 각 α들을 대입하여 w{w_1, w_2, ..., w_n}와 b{b_1, b_2, ..., b_n}를 구한다. 구해진 (w, b, α)쌍에서 α≠0인 지점들을 Support Vector로 구한다.
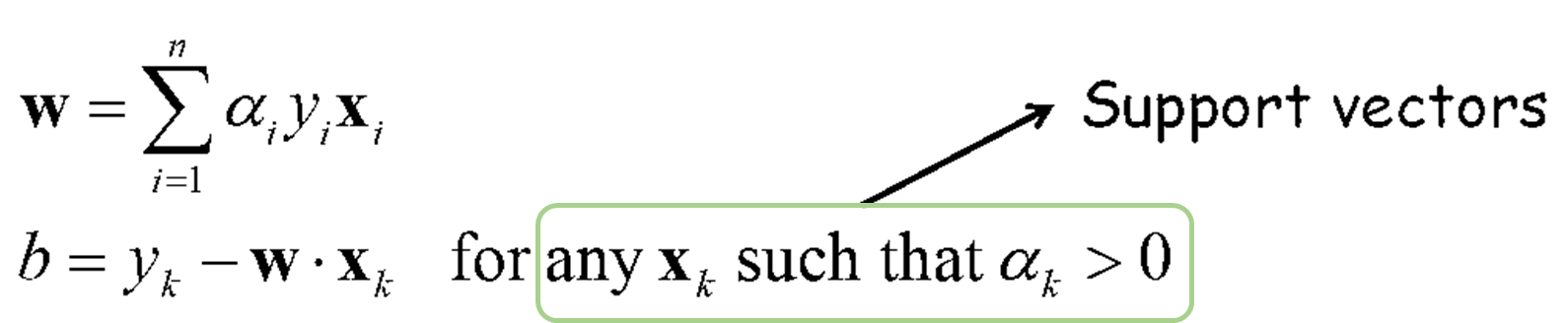
· 이렇게 Dual Form을 완성시킴으로써 얻을 수 있는 점은 다음과 같다.
1) 식을 풀 수 있는 효과적인 알고리즘이 많다.
2) Kernel Trick을 사용할 수 있다.
→ non-linear boundary도 Linear하게 LSVM을 통해 풀이할 수 있는 방법(고차원화)
예제 2
· D = {(1, 1, -1), (2, 2, 1)}에 대하여 α에 대해 Optimization 문제를 풀면 아래와 같이 정리할 수 있다.

· D = {(1, 1, -1), (2, 2, 1)}를 대입하면 아래의 식을 얻을 수 있다.
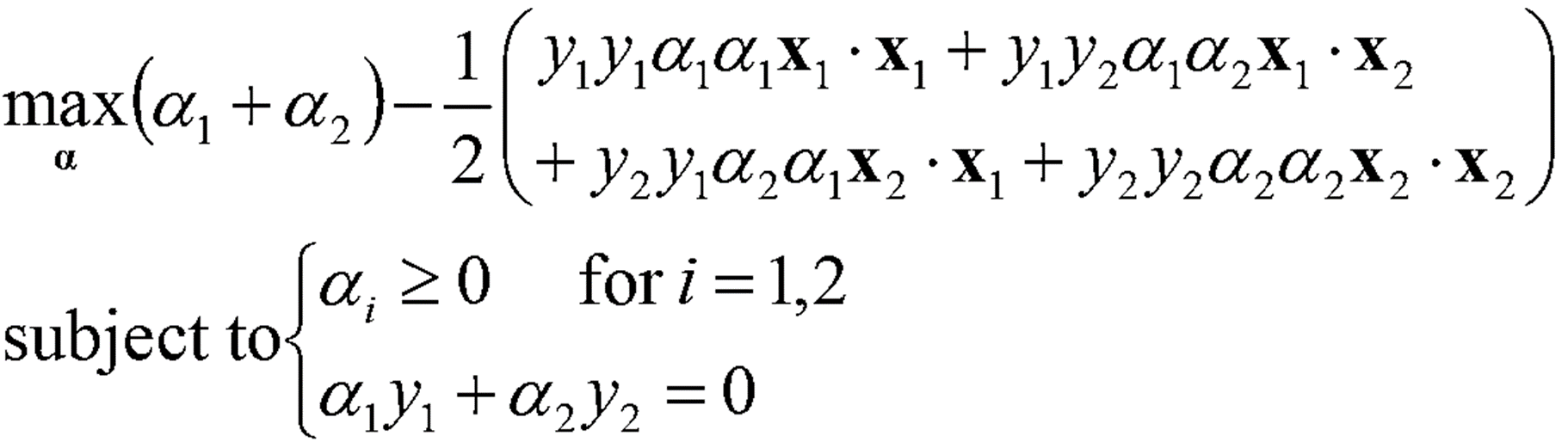
· 식을 정리해보면 아래의 식을 얻을 수 있고, 이를 통해 α_1, α_2를 구할 수 있다.

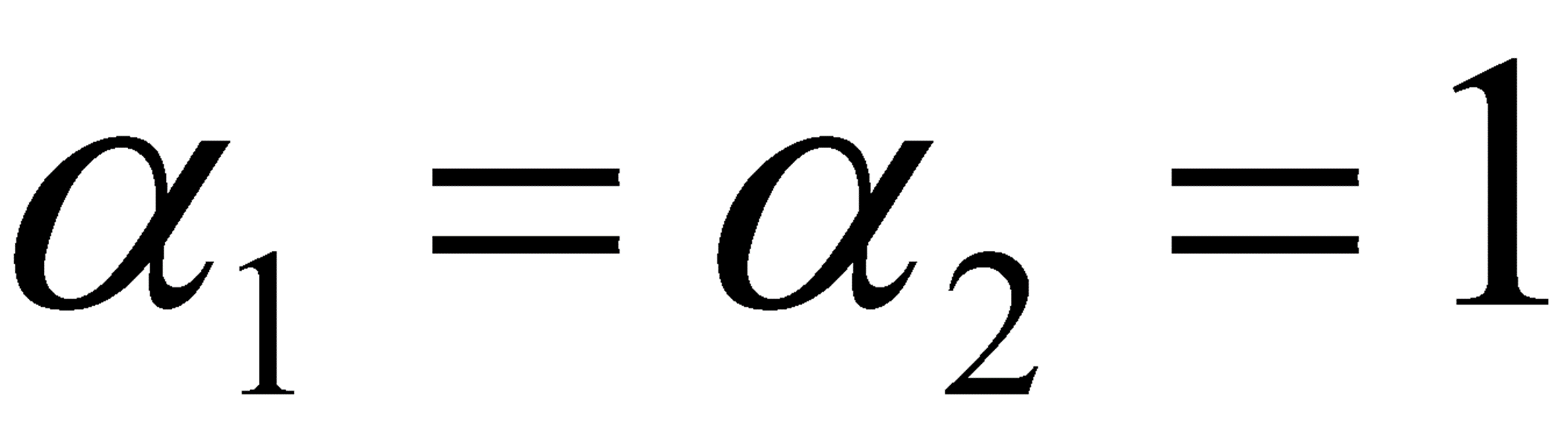
· 위에서 구한 α_1, α_2를 통해 w와 b를 구한다.
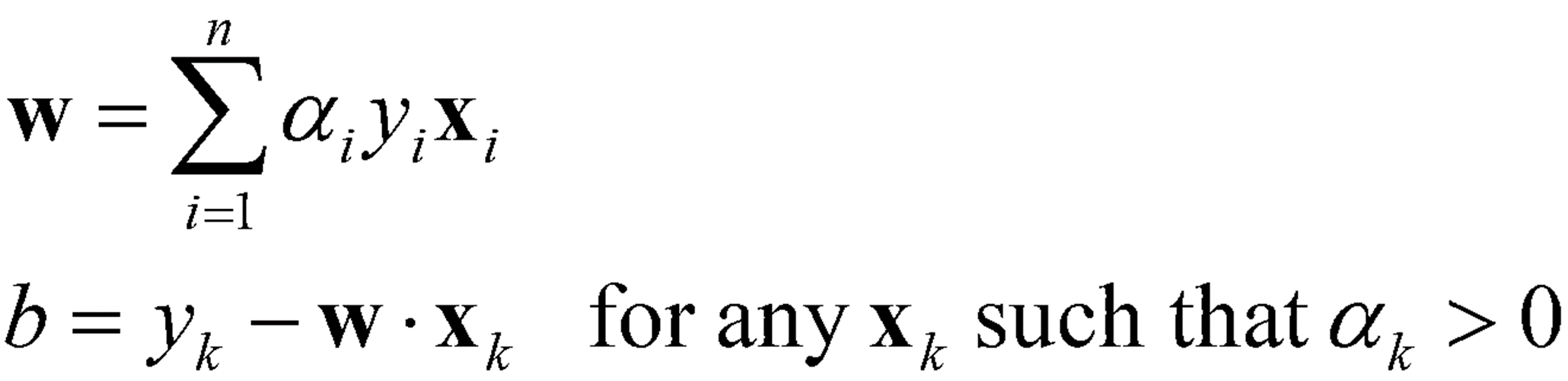

· 결과적으로 Linear Boundary를 구할 수 있다.
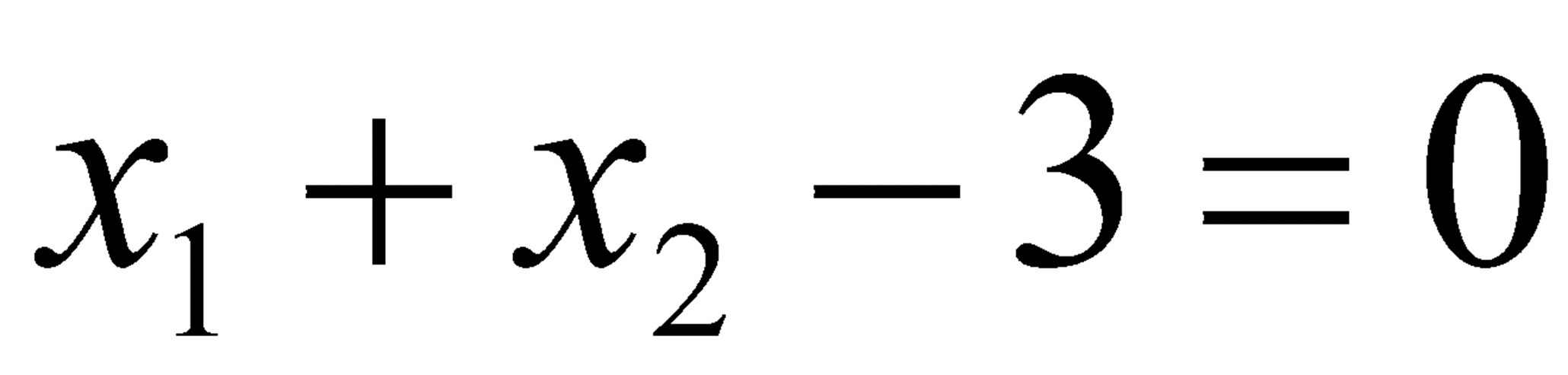
Non-Linear한 Problem은 어떻게 풀 것인가?
1) Soft Margin을 두는 법(Error를 허용하는 법)
2) Kernel Trick(고차원 매핑)
1) Soft Margin을 두는 법
· 각 data x_i에 대해 error ε_i ≥ 0이라고 하면 아래의 식을 얻을 수 있으며, 이러한 Boundary를 구할 때 margin을 최대화하고, error를 최소화하는 경계를 구해야 한다.
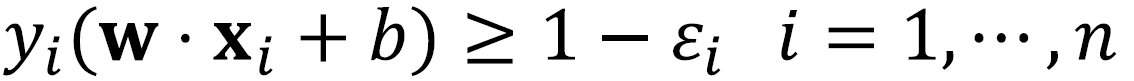
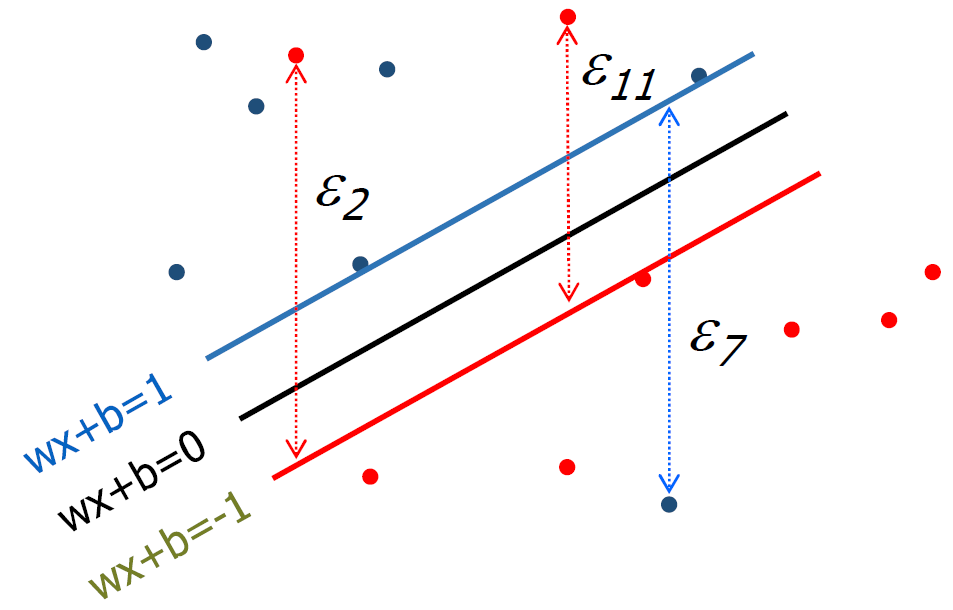
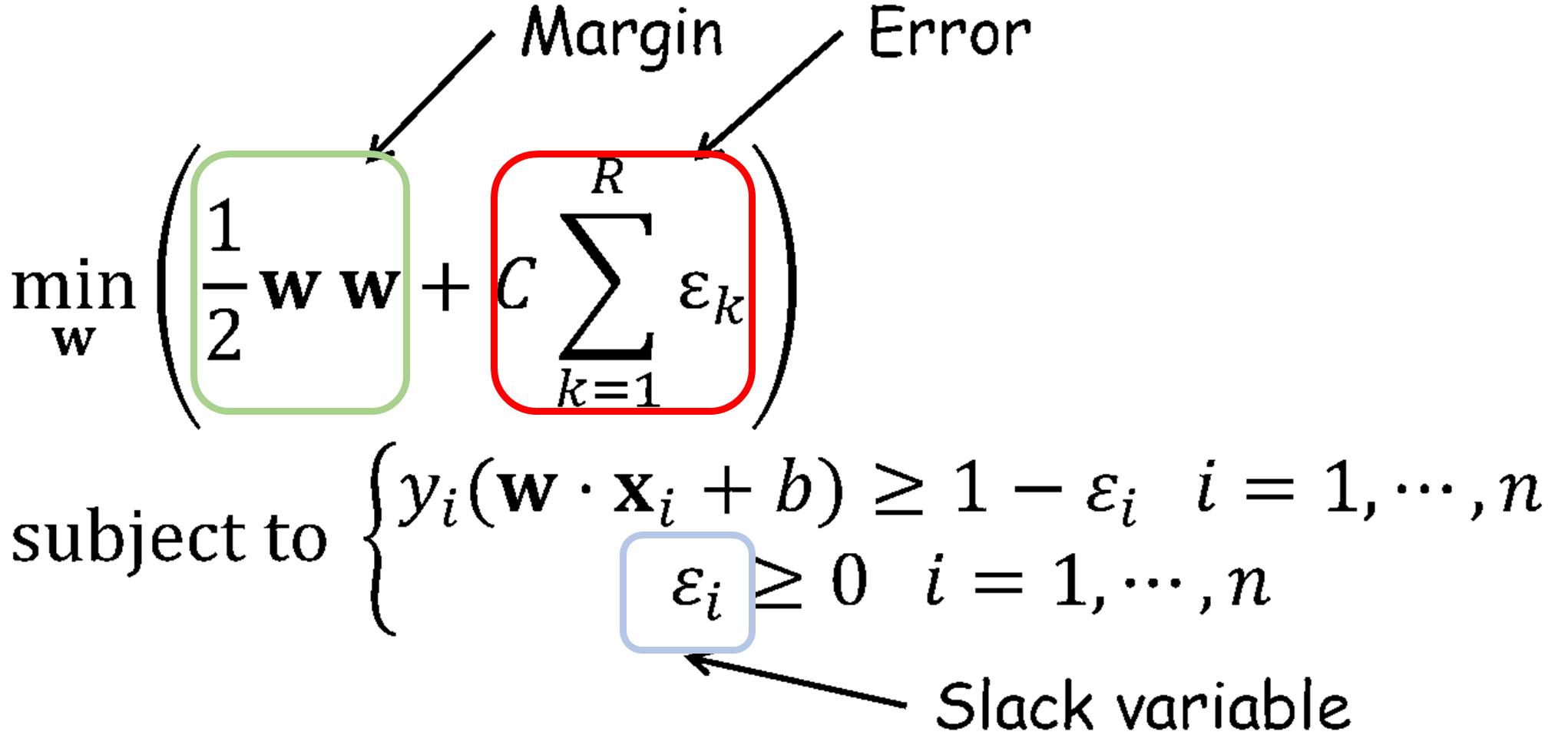
· Error를 포함한 Soft Margin을 둘 때는 아래와 같은 식을 활용할 수 있다. 여기서 C는 에러를 얼마나 허용할지(Controlling overfitting)에 대한 가중치로 전문가(Experts)에 의해 정해진다.
· Error에 대한 조건이 추가되기 때문에 α를 구하기 위한 식은 아래와 같이 가중치(C)가 α의 범위로 지정된다.

· 위 식을 통해 α를 구하고 w와 b는 이전과 동일하게 α를 대입하여 구해내면 된다.
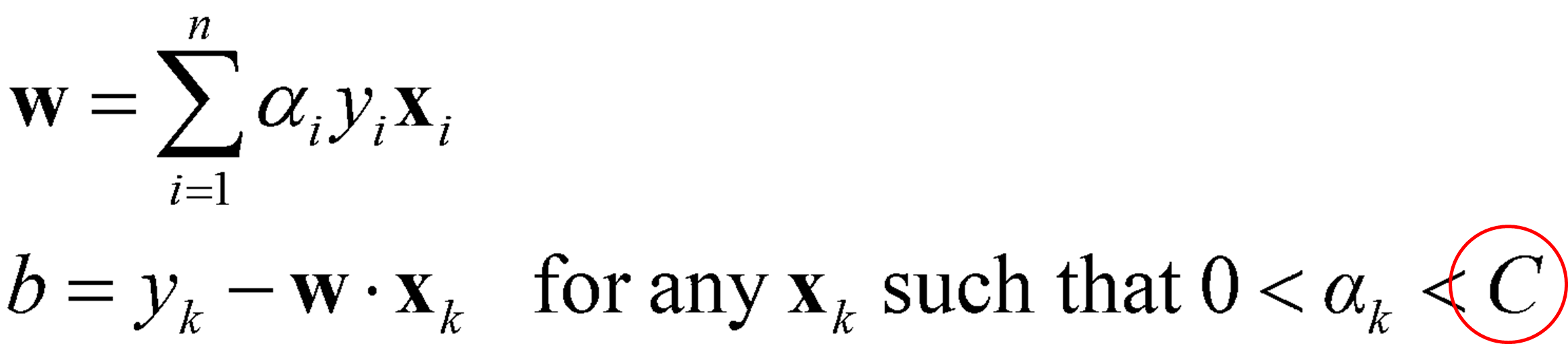
· 가중치 C의 효과에 대해서 세부적으로 정리하면 아래와 같다.
1) C = infinite
- Error를 거의 허용하지 않는다. (Narrow margin)
- Equibalent to hard margin SVM
- Over-fitting
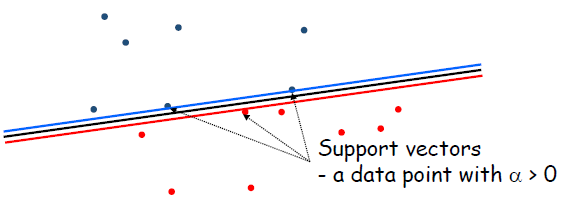
2) C = Some Value
- Error에 대해 일부 허용한다.
- C의 값이 작아질수록 Support vector의 수가 증가한다.
- Support Vector는 margin 위에 있는 points와 내부에 있는 points 두 종류를 모두 가진다.

3) C = 0
- Error 허용의 최대치 (Maximum margin)
- Over-generalization
2) Non-Linear SVM
· 아래 그림은 선형 Boundary로 구분이 가능하다.

· 두 번째 그림 역시 선형 Boundary를 error를 일부 허용함을 통해 생성할 수 있다.

· 그러나 세 번째 그림은 Linear boundary + error로 처리하기에는 무리가 있다.

· Boundary를 아래와 같이 2차원 곡선으로 형성해야 하는 것인지 생각해 볼 필요가 있다.

· 또는 data를 고차원 공간(Higher-dimensional space)에 Mapping하는 방법도 있을 것이다. 여기서는 이 고차원 공간을 사용하는 Kernel trick에 대해서 정리할 예정이다.

· 고차원 공간에 Data를 Mapping하게 되면 같은 데이터라도 아래와 같이 위상차이를 확인할 수 있다.

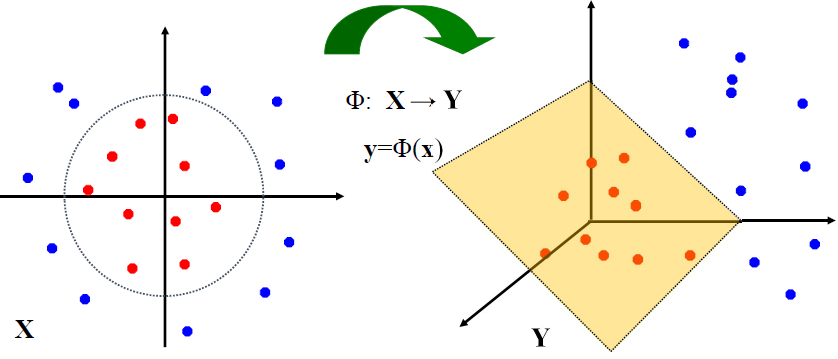
· 이를 식을 통해 표현하려면 어떻게 해야 할까. 앞의 Soft Margin에서 정리했던 식에서 데이터 x_i, x_j의 내적 부분을 Φ:x→Φ(x)를 통해 재정의해야 한다.
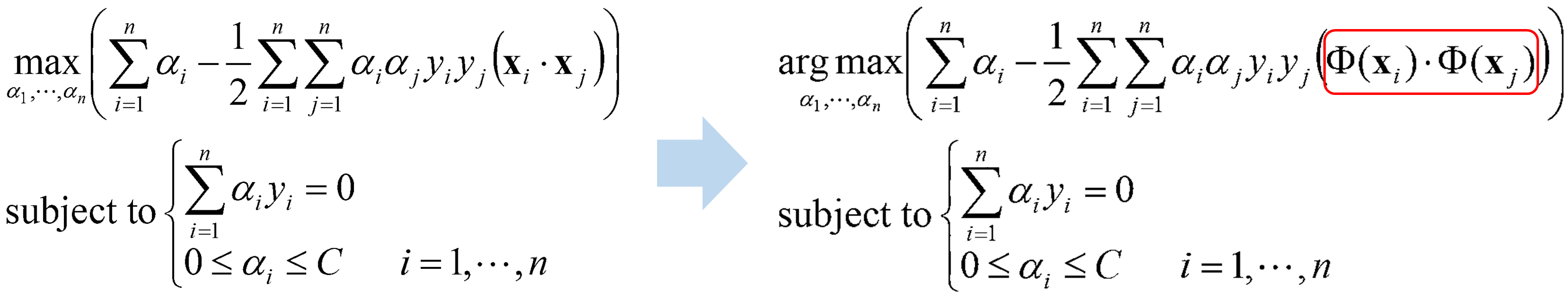
· 위에서 구한 α를 통해 w와 b를 아래와 같이 구한다. 아래 식에서도 마찬가지로 Φ:x→Φ(x) 변환이 이루어졌다.
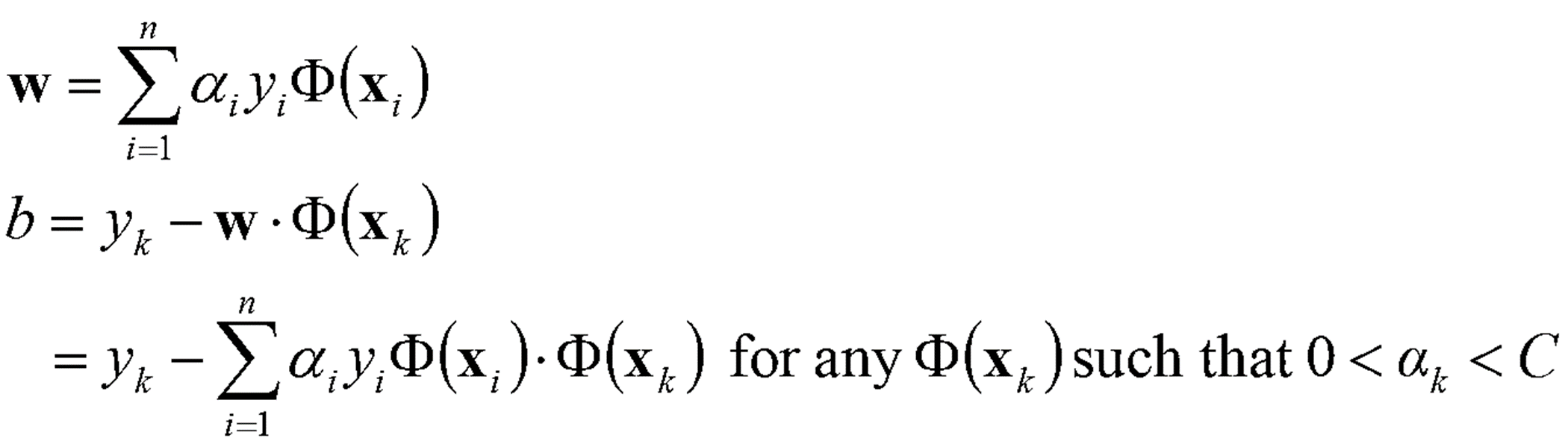
예제 3
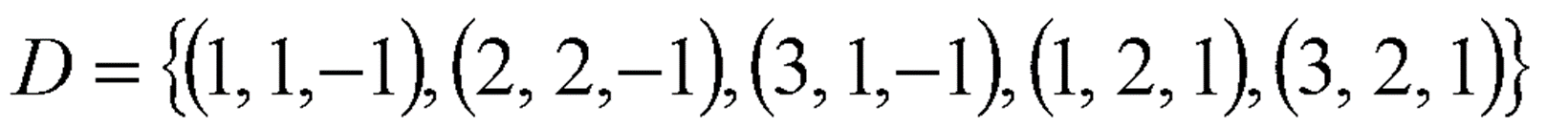
· 데이터가 위와 같이 주어졌을 때, Non-Linear SVM을 적용하기 위해 Data를 변환할 Φ(x)을 임의로 생성해보았다.
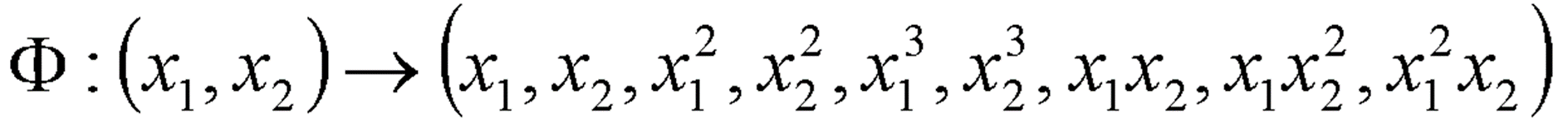
· 이제 이 Φ(x)에 Dataset을 대입하여 Φ(D)를 구한다. 이를 아래 식에 적용시킴으로써 α, w, b를 구한다.

3) Kernel Trick

· 위 예제에서 사용한 Transform Φ(x)를 아래와 같이 변경하면 결과값은 차이가 없지만 계산량을 줄일 수있다.
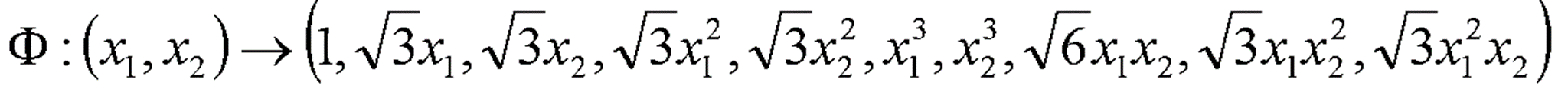
· 위와 같은 mapping 함수를 사용하여 mapping하면 계산량 즉, inner product의 연산량을 획기적으로 줄일 수 있다.

· 만약 위의 mapping 함수를 사용하여 아래의 points에 대해 내적(Inner product)하면
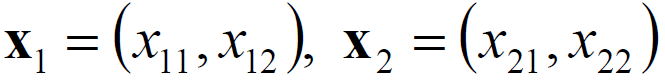
아래와 같이 계산을 수행하면 식이 (x_1·x_2+1)^3 으로 굉장히 간소화 시킬 수 있다.

· 이처럼 잘 디자인된 식을 Kernel이라고 하고 이를 통해 고차원에서도 저차원과 유사한 연산량을 계산할 수 있게 된다.
· ex) x_1 = (1, 1), x_2 = (2, 2)일 때, 아래 ①, ②의 결과값을 비교해보자(답 : 125로 동일함을 확인할 수 있다.)
① 각 Φ(x_1), Φ(x_2)를 구한 후 Inner product한 결과값
② Kernel : K(x_1, x_2) = (x_1·x_2+1)^3 의 결과값
· Kernel 함수는 차원에 따라 아래와 같이 또 다른 mapping 함수도 있다.
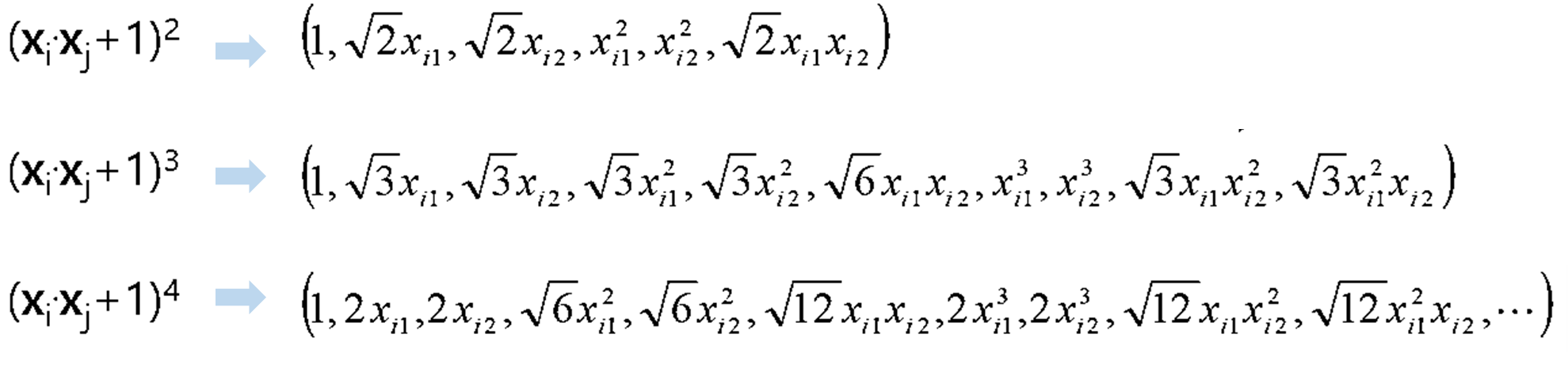
· 만약 x_i, x_j가 m차원이고 (x_i·x_j+1)^k의 kernel을 사용한다면 차원은 (m+k)!/m!k! 이다.
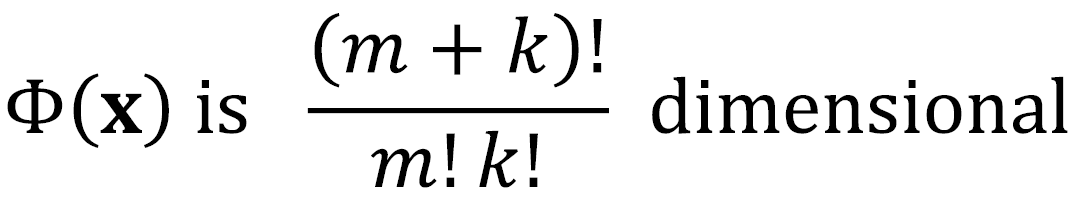
· 앞서 Non-Linear의 식을 Kernel에 대하여 정리하면 아래와 같이 mapping 함수의 내적 Φ(x_i)·Φ(x_j) 부분이 K(x_i, x_j)로 대체 된다. 이를 통해 α를 구한다.

· 계산된 α값으로 아래와 같이 Boundary에 대한 w, b를 구할 수 있다.
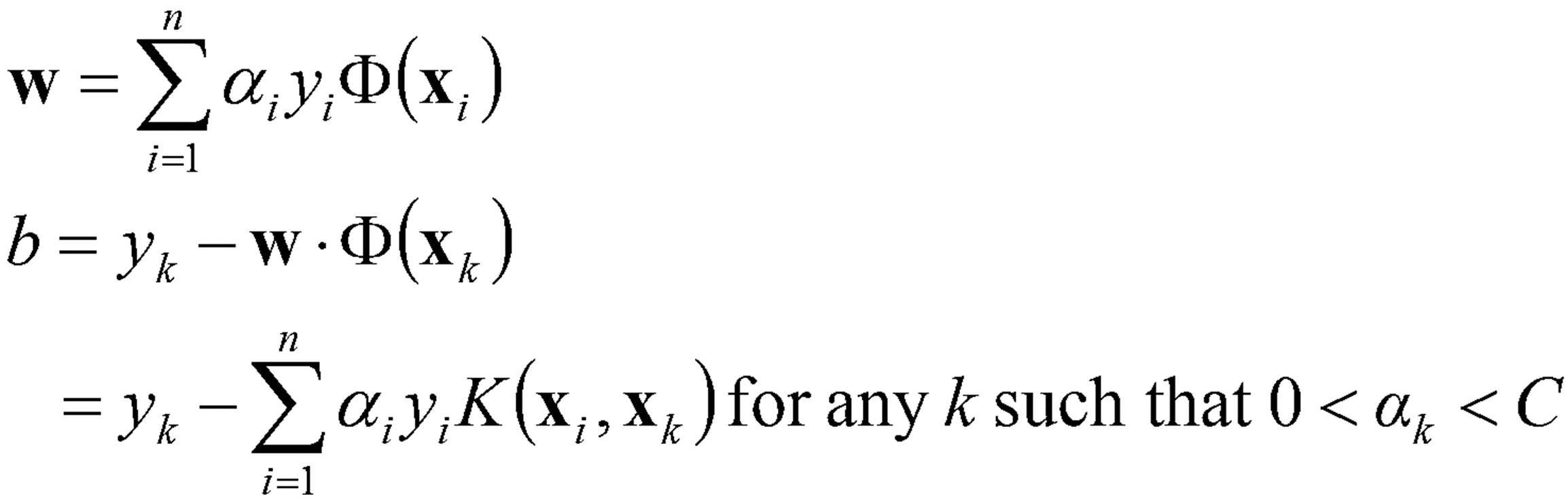
· 일반적으로 자주 사용되는 Kernel Function은 아래와 같다. 이 중에서는 Polynomial Kernel과 Gaussian Kernel이 많이 쓰인다.

→ Homogeneous Polynomial Kernel
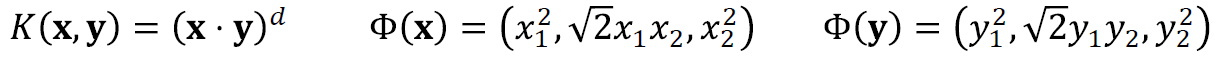
→ RBF Kernel
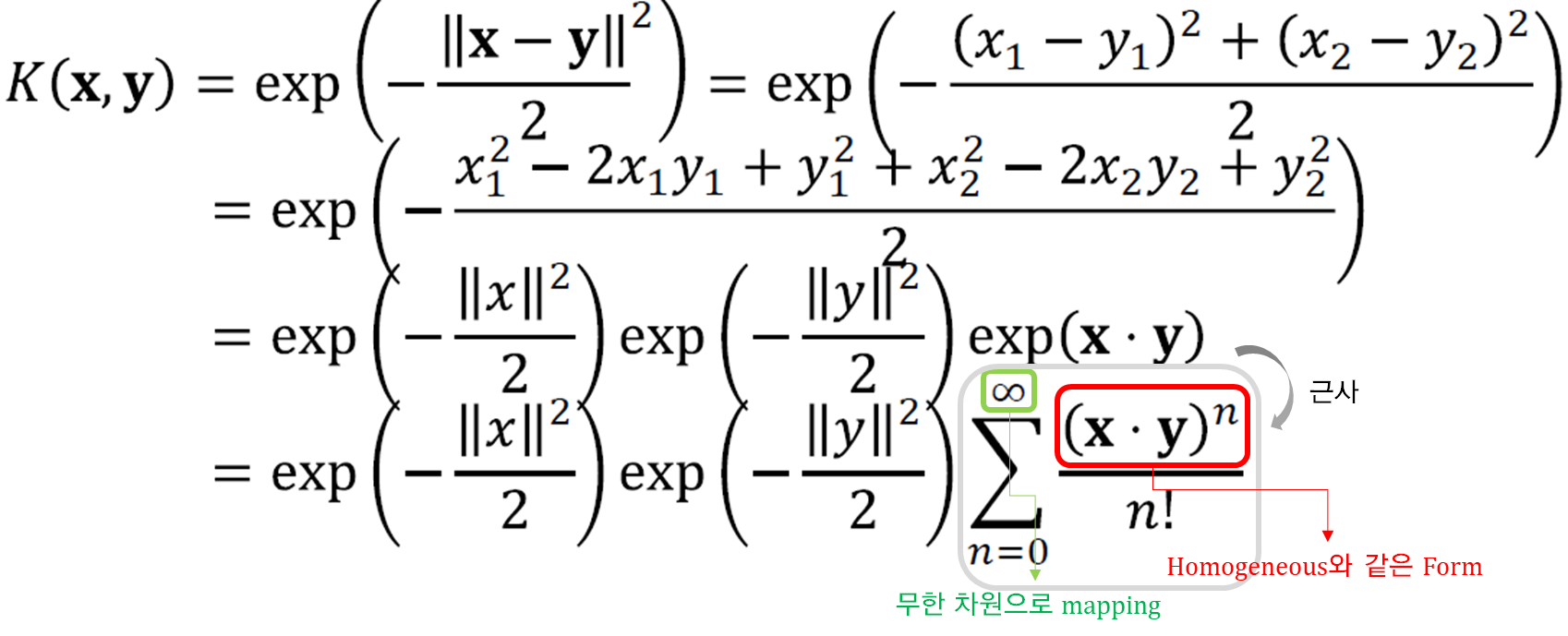
※ 참고) Kernel이 될 수 있는 조건 : Mercer's Condition

예제 4
· 아래와 같은 분류 문제(Red, Blue)가 있을 때, d = 2로하여 Kernel을 아래와 같이 구성하면
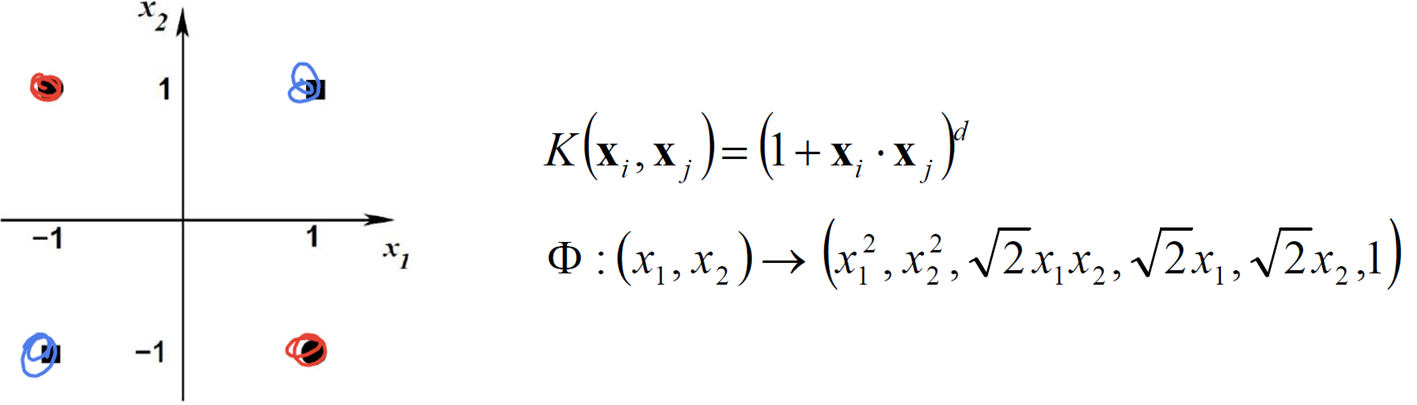
· 아래와 같이 Φ(x_i)를 보면 3, 4, 5번째 인자만 값이 1이 아니므로 3차원의 공간에 표현이 가능하게 된다. 그리고 이를 구분하는 hyperplane을 그려서 linear boundary를 그릴 수 있다.

· Dual Form Formulation을 통해서 식을 풀어볼 수 있다.

· 아래와 같이 식을 생성하고, 조건 내에서 Quadratic programming으로 풀이한다.

· Quadratic programming을 통해 식을 만들어내면 아래와 같이 정리된다. 왼쪽의 식을 통해 α를 구하고 우측 식으로 Boundary(w, b)를 구할 수 있다.
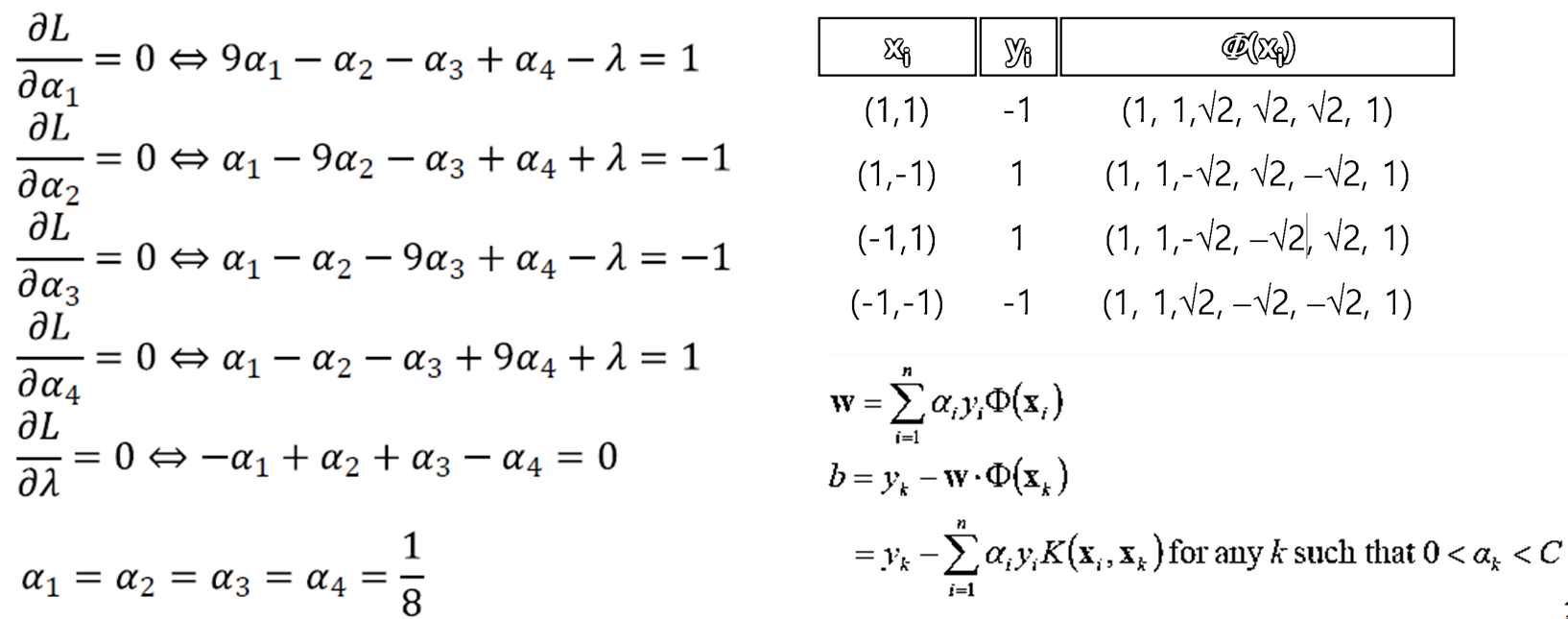
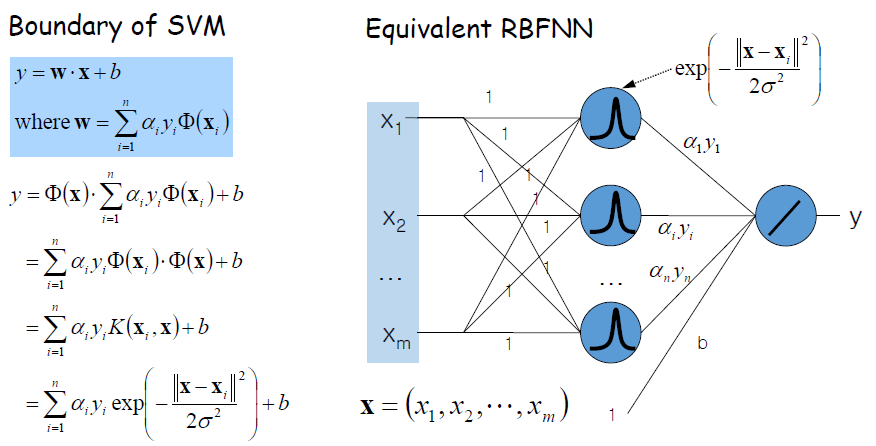
SVM with RBF Kernels vs. RBFNN
· RBF Neural Net : Activate Function을 RBF(Gaussian Function)로 하는 것을 말한다.
· 아래 그림은 SVM으로 Boundary를 만드는 것이 RBFNN과 동일하다는 것을 보여준다.
SVM의 장/단점
· 장점
- Optimal한 Hyperplane을 찾아내는 방법으로 잘 동작한다.
- Kernel trick을 이용하면 데이터를 고차원으로 바꾸어도 잘 동작한다.
· 단점
- 기본적으로 Binary Classification만을 다룬다.
- Hyperparameter를 선택해주어야 한다. (C, k)
- 메모리와 CPU time에 많은 비용이 든다.
- Constrained Quadratic Programming을 푸는 데 Stability Problem이 있다.
Steps to use SVM
1) Kernel Function 선택 : RBF 커널이 주로 사용됨, 적절한 파라미터 선택(k-fold validation 활용)
2) C값을 선택(k-fold validation 활용)
3) Quadratic programming problem을 풀이
4) support vector로 부터 Discriminant function 생성, Discrimate 수행
'DataScience > 머신러닝' 카테고리의 다른 글
| 머신러닝 :: Constrained Optimization (0) | 2023.04.27 |
|---|---|
| 머신러닝 :: Naive Bayesian (0) | 2023.04.26 |
| 머신러닝 :: Logistic Regression, Gradient Descent Method (1) | 2023.04.25 |
| 머신러닝 :: New Interpretation of Linear Regression(MLE) (0) | 2023.04.24 |
| 머신러닝 :: Model Optimization, Evaluation, Cross Validation (0) | 2023.03.21 |




댓글