
머신러닝 :: 6. Logistic Regression, Gradient Descent Method
Logistic Regression
· Classification을 위해 Logistic function(=Sigmoid function)을 사용하며, 0~1사이의 값으로 Regression한다.
→ 이는 0이냐 1이냐를 정하는 Binary class를 classification하는데 확률값처럼 사용이 가능하다.
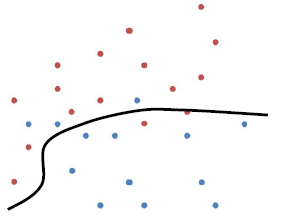
· Logistic Regression은 아래와 같은 선형 분류기를 더 soft하게 바꾸는 데에서 출발한다.
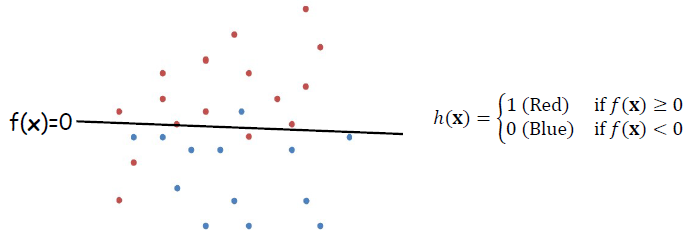
· 위 그림에서의 classifier h(x)는 hard boundary(0 또는 1)를 형성하고 있다. h(x)를 아래와 같이 sigmoid function을 적용하여 soft boundary로 변경할 수 있다.

· 여기서 h(x)는 0~1사이의 continuous한 value를 output으로 출력하기 때문에, probability와 대응이 가능하다.
즉, 각 클래스에 대한 확률 P로 아래와 같이 변경할 수 있다.
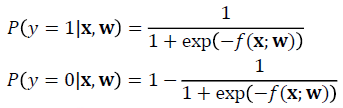
or
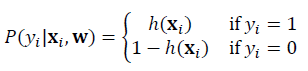
· 아래와 같은 조건일경우, 최적의 분류기 f(x)를 찾기 위해 Gradient descent method를 사용할 수 있다.

· 위 식에서 P(D|w)는 아래와 같은 순서로 P(y_i|x_i, w)와 같이 변환할 수 있다.
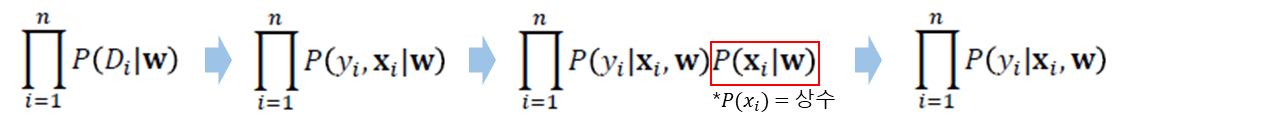
· 분류해야 할 2개의 Class가 각각 Red, Blue일 경우, Red point는 Red일 확률이 높도록, Blue point는 Blue일 확률이 높도록 아래의 식을 최대화하는 Boundary(가중치 w값)를 찾는다. 식의 좌측은 Red를 Red라고 예측할 확률, 우측은 Blue를 Blue라고 예측할 확률을 말한다.
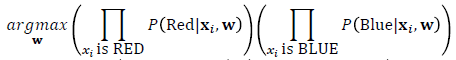
· 각 클래스를 예측했을때의 확률값은 아래와 같의 표현할 수 있다.
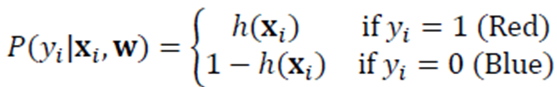
· 이를 위의 식에 적용하여 식을 풀어보면


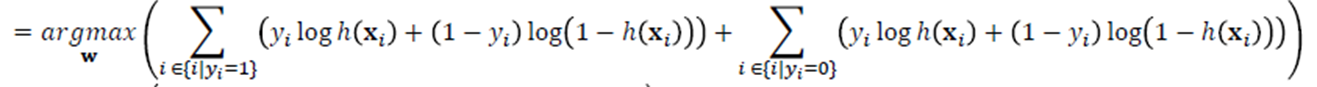
· 결과적으로 아래의 식을 최대화 하는 w값을 찾는 것으로 정리할 수 있다.
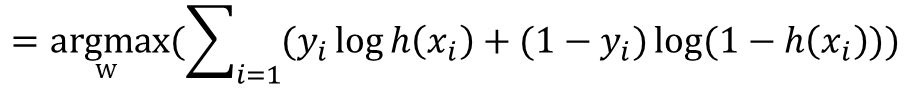
· 이 식은 Gradient Descent Method를 활용하기 위해 아래와 같이 최소화하는 w값을 찾는 식으로 변환이 가능하다.(-를 식 앞에 붙임으로써 log 안의 값의 분자/분모를 바꾸어주는 것으로 이해하면 쉽다.)
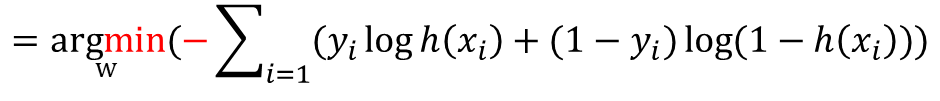
· 이 때 h(x)는 sigmoid 함수가 사용되며, 아래와 같이 표현된다.
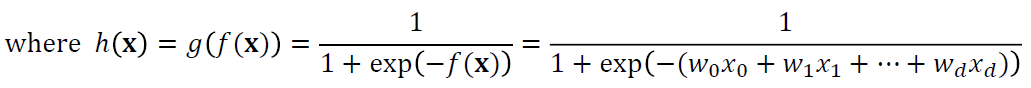
·

· Gradient Descent Method를 통해 미분하며 E(w)의 최솟값을 찾아나간다. 이 때 f(x)와 h(x)는 미분시 아래와 같이 정리될 수 있으며, 이를 통해 E(w)를 아래와 같이 풀이할 수 있다.
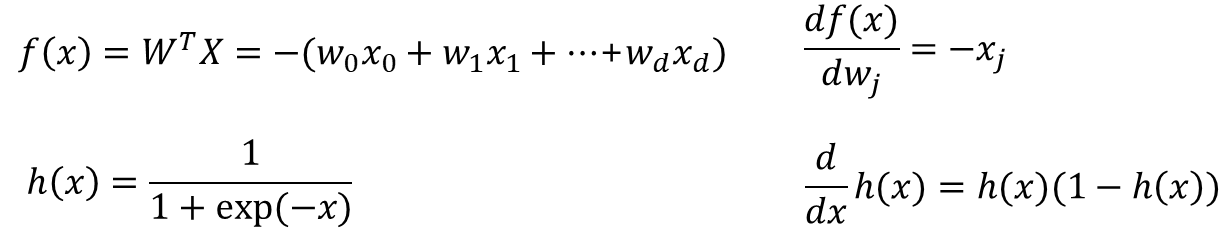

· 전체 식은 아래로 정리된다.
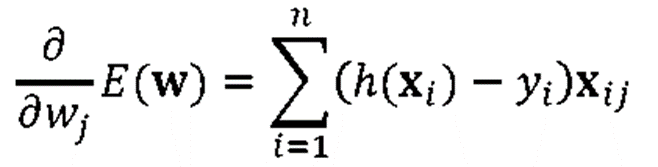
· Logistic Regression을 위해 아래처럼 Greadient Descent를 learning rate(η, etha)간격으로 반복하여 최솟값을 찾아간다.
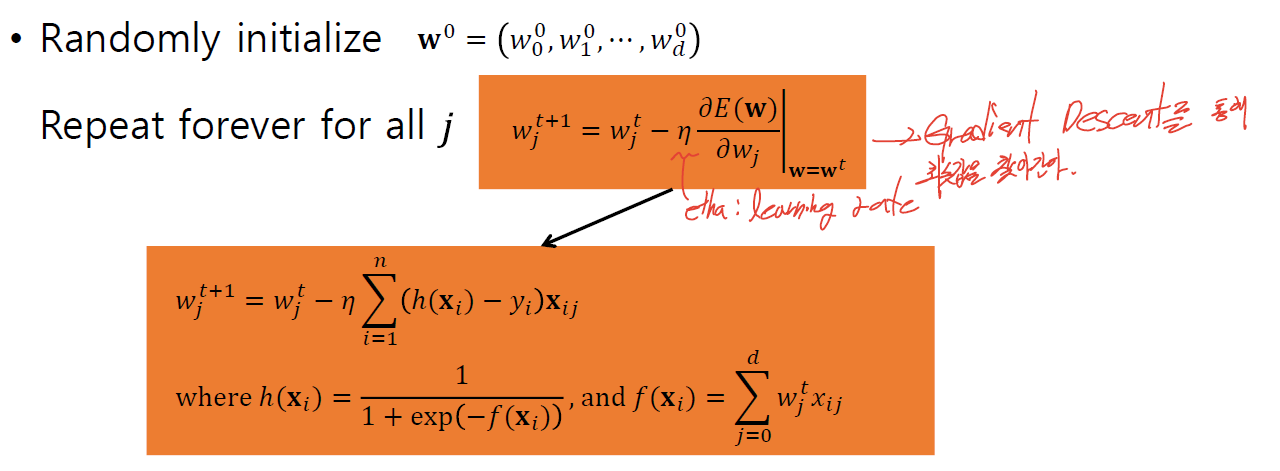
· Logistic Regression은 Neural Network의 Simplify된 Version으로도 볼 수 있다.
- No closed form solution(Optimized by Gradient Descent method)
→ Global optimum인지는 알 수 없고, Local optimum을 주어진 조건 내에서 푸는 문제를 말한다.
- A linear boundary
→ Neural network에서 weighted sum을 통해 non-linear function을 저장하고, 이러한 non-linear function으로 hidden layer를 쌓는다. 이를 통헤 output으로 Boundary를 만드는데 이 때 non-linear 층 경계가 만들어진다.
- Binary classifier : AND 조건을 추가하여 multi-class에 대한 분류도 가능하다.

'DataScience > 머신러닝' 카테고리의 다른 글
| 머신러닝 :: Constrained Optimization (0) | 2023.04.27 |
|---|---|
| 머신러닝 :: Naive Bayesian (0) | 2023.04.26 |
| 머신러닝 :: New Interpretation of Linear Regression(MLE) (0) | 2023.04.24 |
| 머신러닝 :: Model Optimization, Evaluation, Cross Validation (0) | 2023.03.21 |
| 머신러닝 :: Linear Regression(선형 회귀식 풀이법, SLE) (0) | 2023.03.20 |




댓글