
머신러닝 :: 8. Constrained Optimization
Constrained Optimization
· Constrained Optimization은 제한이 걸린 상황에서 최적화문제를 푸는 방법으로 SVM(Support Vector Machine)을 알아보기 전에 알아두어야 할 개념이다. 즉, 제한이 있는 input(x 또는 아래 그림의 w)에 따른 최적화 문제를 푸는 것이다.
· 이를 수식으로 풀어보기 위해 먼저 f(x)가 n차원 공간의 함수일 때, 즉 w = (w_1, w_2, ..., w_n)일 때 아래처럼 표현된다.

· 이 때 equality constraint(g_j(w))와 inequality constraint(f_j(w))는 아래와 같이 convex(아래로 볼록)하다고 가정한다.

· 맨 위의 수식을 풀기위해 Lagrange Function을 활용할 것이다.

· 위의 Lagrange Function을 적용하기 위해 식을 아래와 같이 변형하고, F(x, λ, α)에 적용한다.

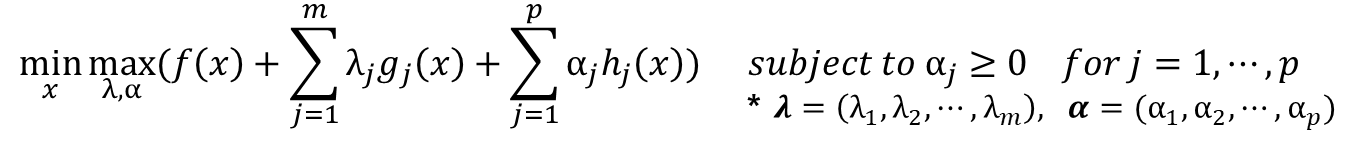
· 아래의 Condition을 만족하는 결과값을 찾고, 그 결과를 위의 식에 적용 후 만족하는 값들을 찾아 최종 Solution을 만든다.
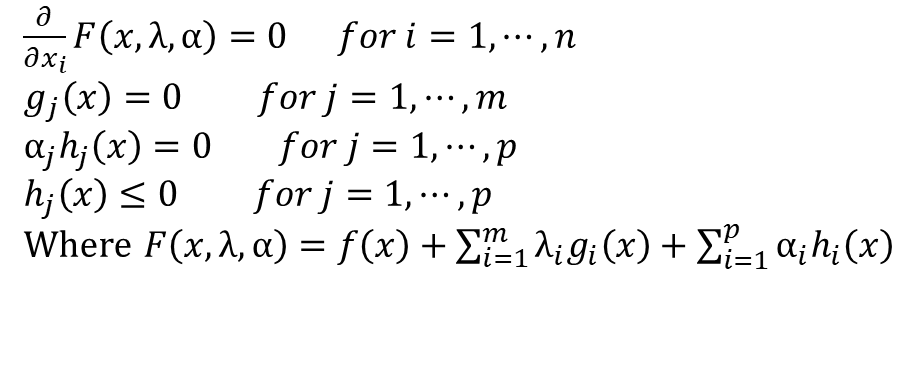
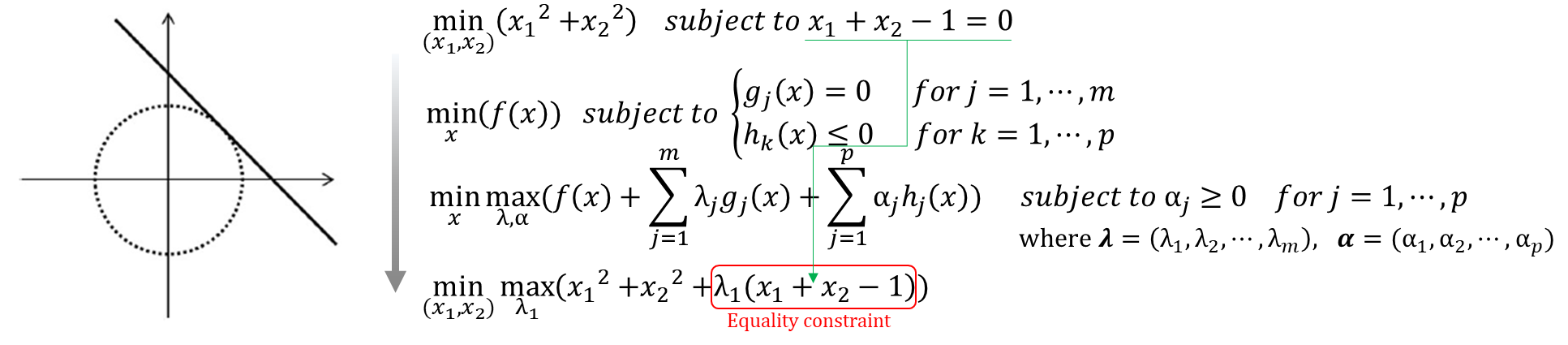
예시 1
· 아래와 같이 원에 접하는 접선의 직선을 구할 때 subject to x_1+x_2-1=0이라는 constraint 조건을 갖고 문제에 접근한다. 여기서는 Equality Constraint하나만 있기 때문에 Equality constraint를 추가해준 것이다.
· 위에서 도출한 식을 미분하여 아래 Condition을 만족하는 대표 해(candidates)를 찾는다.
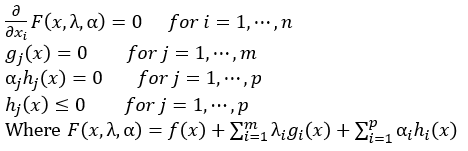
· 도출된 3개의 식을 통해 x_1, x_2, λ_1을 구한다.

예시 2

· 위와 같이 Inequality Condition을 감안한 문제를 예시1과 동일하게 풀이해보면 아래와 같다.
KKT Multiplier를 기준으로 문제를 나누어 풀 수 있다.

· How to easily solve
1) Divides into sub-problems using KKT multipliers
2) Solve equations in each sub-problem
3) Check whether the solution satisfies inequalities
Lagrange Multiplier Method for Constrained Optimization
· 아래의 경우 잘 동작한다.
- f(x)가 2차원(2nd order)일 경우
- g_j(x)와 h_j(x)가 선형(linear)일 경우
· 만약 Inequality Condition이 p개 있을 경우, 최악의 경우 2^p 세트의 Equation을 풀어야 할 수 있다.(In the worst case)
Dual Form
· 아래의 두 식의 결과는 동일하기 때문에 바꾸어 풀 수 있다. 이 Form은 다음 포스팅 SVM을 설명할 때 쓰일 예정이다.
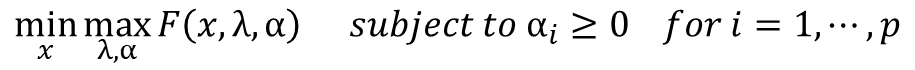

'DataScience > 머신러닝' 카테고리의 다른 글
| 머신러닝 :: Support Vector Machine (0) | 2023.04.28 |
|---|---|
| 머신러닝 :: Naive Bayesian (0) | 2023.04.26 |
| 머신러닝 :: Logistic Regression, Gradient Descent Method (1) | 2023.04.25 |
| 머신러닝 :: New Interpretation of Linear Regression(MLE) (0) | 2023.04.24 |
| 머신러닝 :: Model Optimization, Evaluation, Cross Validation (0) | 2023.03.21 |




댓글