
머신러닝 :: 5. New Interpretation of Linear Regression
Linear Regression
· 아래와 같은 데이터셋에서 Best fit한 line f(x)을 찾으려면 Linear Regression을 수행할 수 있다.
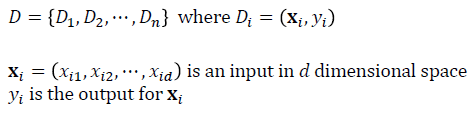
· 지난 포스팅에서 다뤘던 Linear Regression에서는 Squared Error E(w)를 최소화하는 f(x)의 coefficient, 즉 w(weight)를 찾음으로써 Given Data set에 Best fit한 Line을 찾는다.

· 또 다른 접근방법을 생각해보자. Data set D를 관측하는 확률(Probability)을 최대화하는 f(x)를 찾는다면 아래와 같이 표현이 가능하다. 아래는 f(x)가 given일 경우 Data D가 나타날 확률을 나타낸다. 하지만 아래의 식은 f(x)를 알지 못하기 때문에 활용하기 어렵다.
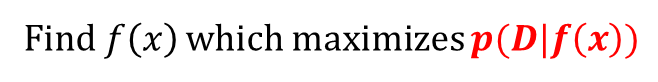
· 위 식을 Bayesian rule에 의해 아래와 같이 변경하여 f(x)를 예측하는 문제로 바꾸어 풀이하는 것이 더욱 편리한 방법이다.
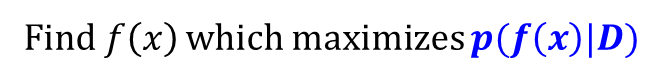
MLE(Maximum Likelihood) of Linear Regression
· Probabilistic model을 위한 가정
- Linear model f(x)로 부터 Normal Distribution에 따라서 Random Noise(ε)가 있는 Data가 생성되었다고 가정한다.

· 위 그래프에서 x_i, f(x), σ가 주어졌을 때, y_i가 관측될 확률밀도함수 P는 아래와 같이 표현 가능하다.

· n개로 이루어진 Dataset D가 아래와 같고, f(x), σ가 주어졌을 때, D의 확률밀도 함수 P는 아래와 같이 표현 가능하다. (이때, 각 샘플(x_i와 x_j)은 서로 독립이며, x_i는 w와 σ에 대하여 독립이다.
· 생성모델인 f(x) (즉, w, σ)로부터 어떤 Data(D)가 나타날 확률 P를 maximize시키는 방법으로 Linear Regression을 접근
→ Maximum Likelihood


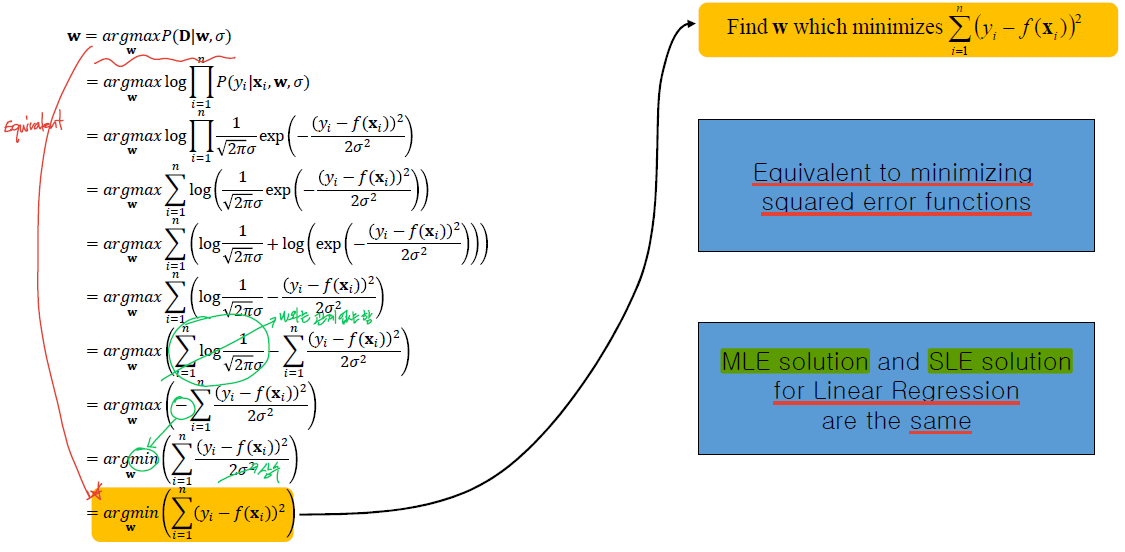
· P(x_i)가 Constant라고 가정하였을 때, D에 대한 확률밀도 함수는 아래와 같이 풀이할 수 있으며, 이를 통해 error를 최소화하고(Minimizes the error), D를 관측할 확률을 최대화(Maximizes the probability)하는 모델을 선택하면 된다.

'DataScience > 머신러닝' 카테고리의 다른 글
| 머신러닝 :: Naive Bayesian (0) | 2023.04.26 |
|---|---|
| 머신러닝 :: Logistic Regression, Gradient Descent Method (1) | 2023.04.25 |
| 머신러닝 :: Model Optimization, Evaluation, Cross Validation (0) | 2023.03.21 |
| 머신러닝 :: Linear Regression(선형 회귀식 풀이법, SLE) (0) | 2023.03.20 |
| 머신러닝 :: k-NN for Classification, Regression (0) | 2023.03.20 |




댓글