
머신러닝 :: 3. Linear Regression
Linear Regression
· 선형회귀(Linear Regression)는 데이터에 가장 잘 맞는(Best Fit) 선을 찾는 것을 말한다.
· 입력값에 대한 출력값이 정해진 지도학습(Supervised Learning)이다.

Best Fit의 의미는 무엇인가?
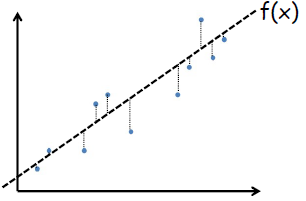
· 모든 i에 대해서 모델 f(x_i)가 데이터 y_i와 가능한한 가장 가깝게 위치하는 것
· 실 Data와 '차이의 절대값'의 합이 최소가 되는 f(x)를 찾는 것
· Error Function E(w)를 최소화하는 가중치 w를 찾는 것

E(w), Error Function을 최소화하는 가중치 W 구하기
· Error Function은 아래와 같이 오차의 제곱(Squared error)으로도 변환할 수 있다.

· 위 식에서 모든 w_i에 대해 각각 편미분을 해서 0을 만드는 지점이 최소값이 된다.
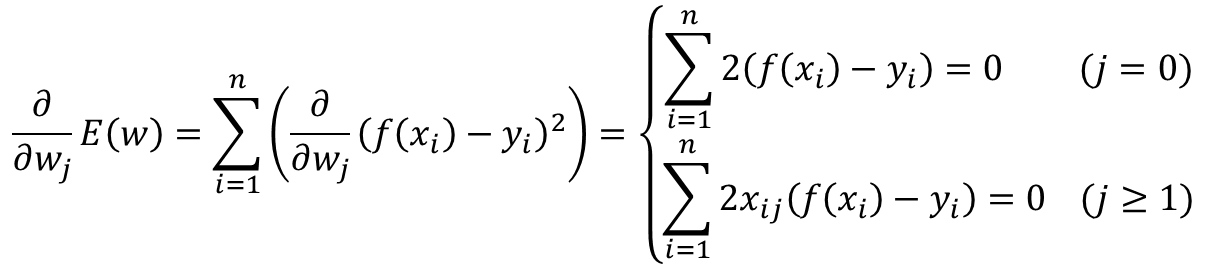
· 위 식을 통해 d개의 식을 얻을 수 있으며, 변수가 d개이므로 연립방정식을 통해 해를 구할 수 있다.
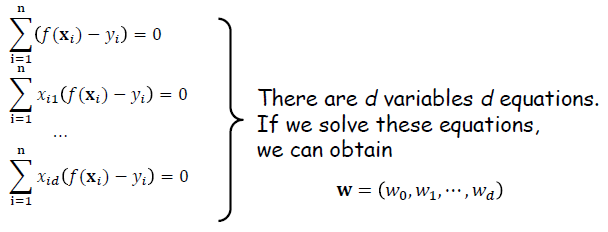
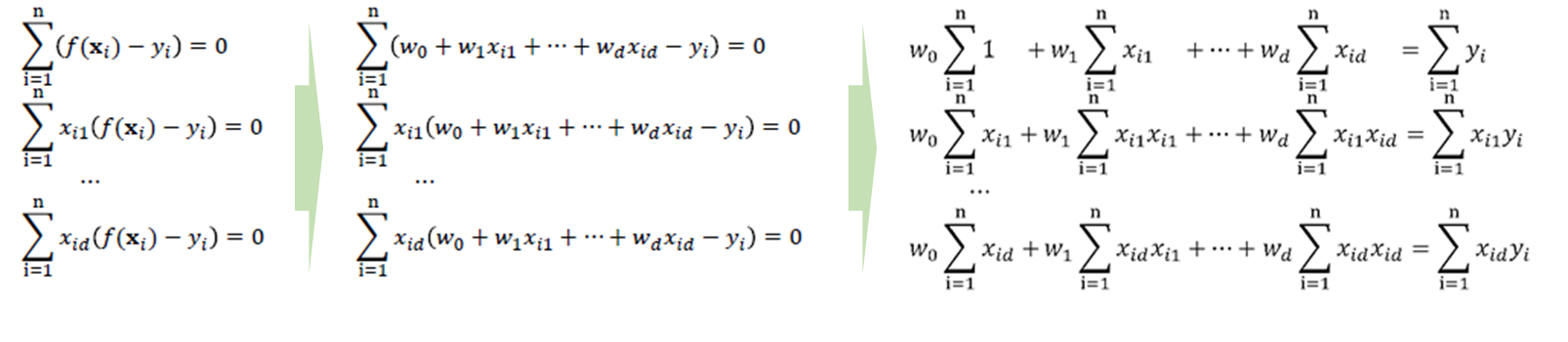
· 식이 복잡해지므로 아래와 같이 행렬식으로 변환해본다.
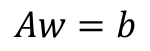
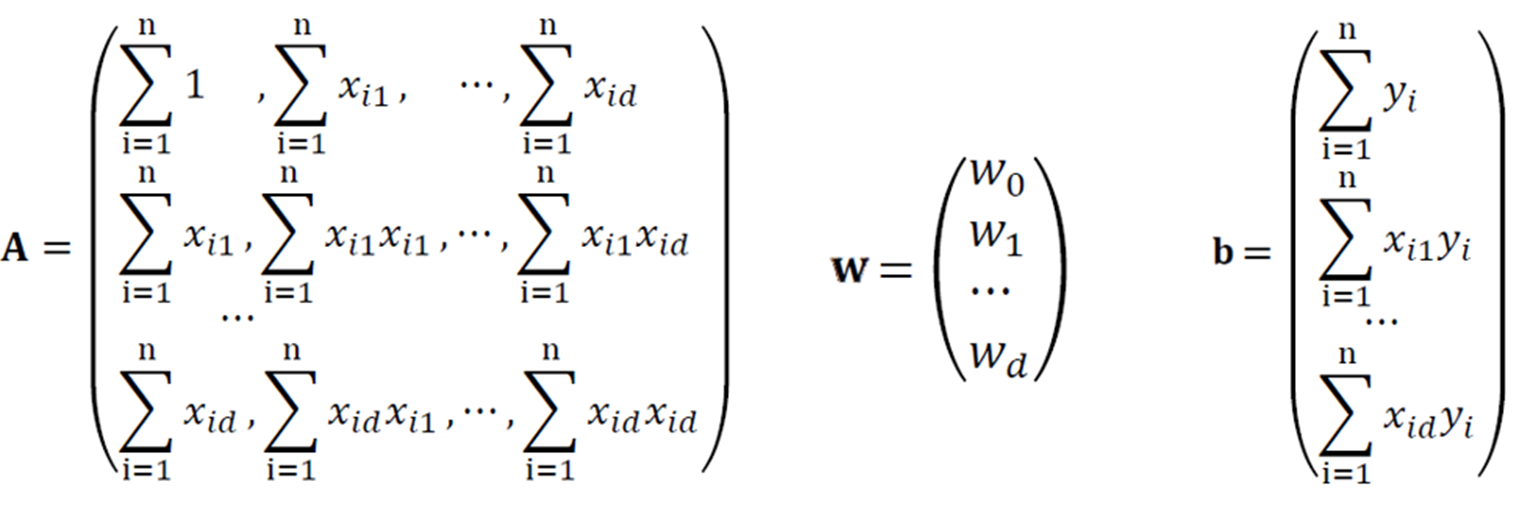
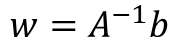
· 위의 행렬식 A의 첫번째 행, 열을 살펴보면 x_i0가 1이기 때문에 다른 원소들과 다른 모습을 보인다. 각 원소에 크기가 1인 x_i0를 곱해주어 이를 통일화 시켜줄 수 있다.
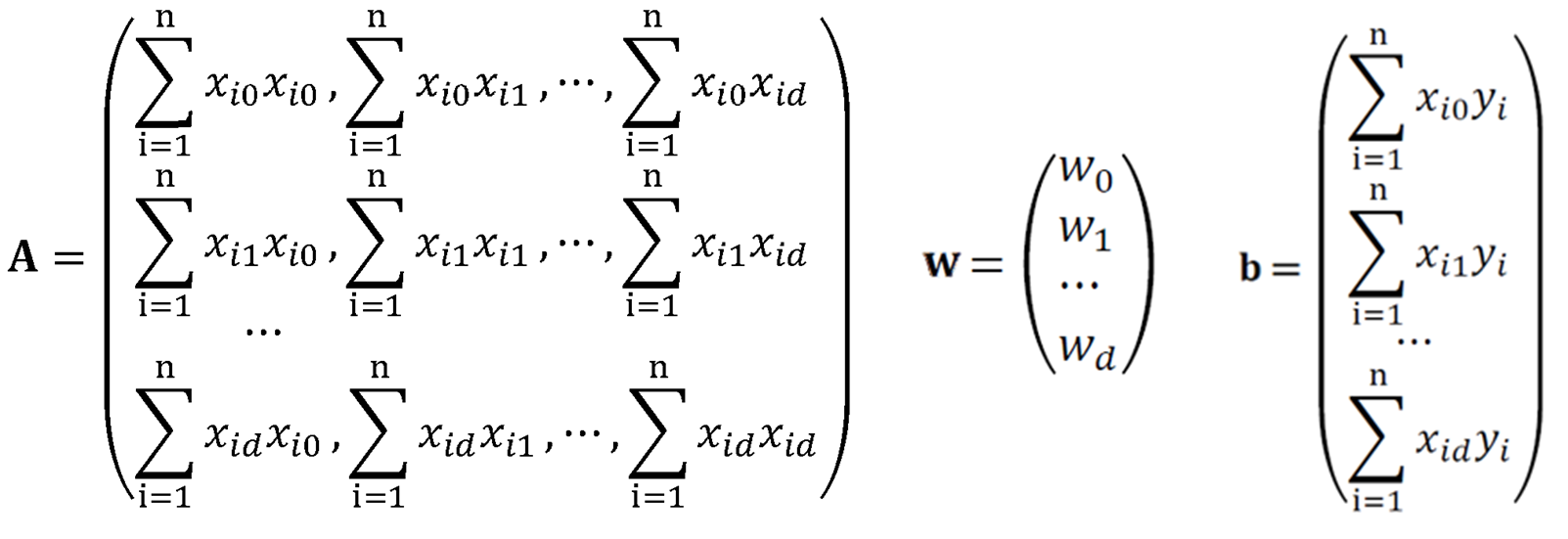
· 행렬 A와 b벡터의 원소인 x, y를 활용하기 위해 아래와 같은 행렬 X, Y가 있다고 정의해보자.

· 행렬 X를 전치시킨 전치행렬을 활용하여 아래와 같이 표현할 수 있다.


· 이제 위 식을 이용하면, Input(X value)과 Output(Y value)데이터만 있다면 활용하여 가중치 W를 구할 수 있다.
Generalized version of Linear Regression
· 선형회귀의 일반화는 기존에 썼던 변수 x를 미리 정의되어 있는 함수 h(x)로 변환하는 것이다. 아래와 같이 상황에 맞추어 적합한 h(x)를 선택하여 적용한다.
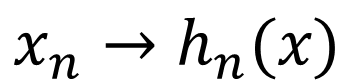
1) Linear Regression
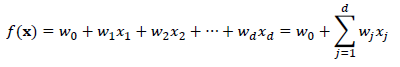
↓

2) Polynomial Regression (2nd order)

3) Polynomial Regression (3nd order)

4) Polynomial Regression (periodic)
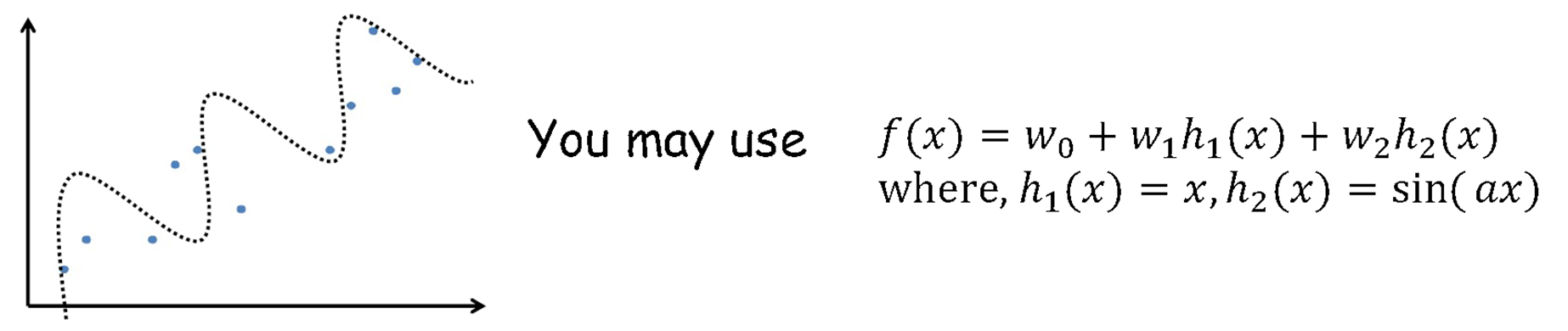
5) Kernel Regression
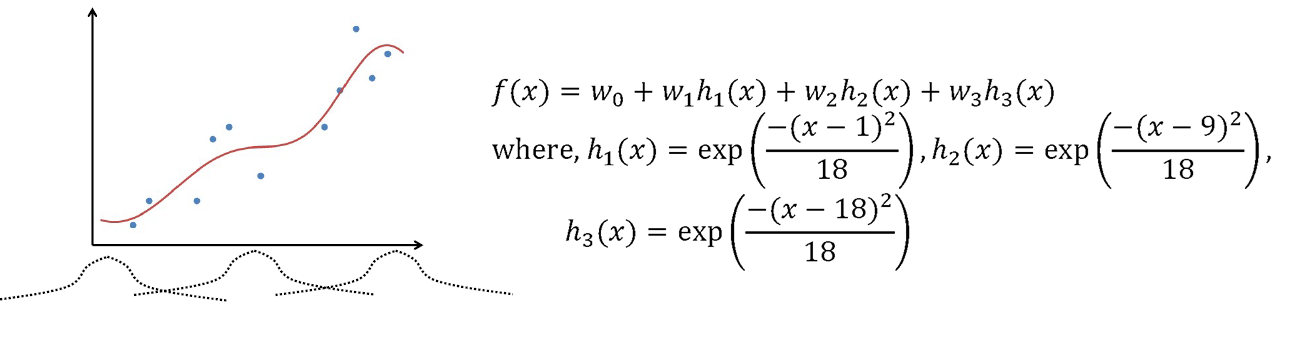
· 이러한 선형회귀 식을 풀때는 앞서 Linear Regression에서 사용했던 방법과 동일하게 Error Function을 최소화하는 가중치를 찾으면 된다.

· k개의 연립방정식은 아래와 같이 행렬식으로 변환해준다.

· 행렬의 원소인 h(x), y를 활용하기 위해 아래와 같은 행렬 H, Y가 있다고 정의해보자.

· 위 식은 아래와 같이 간소화 할 수 있으며, 이를 통해 가중치 W에 대한 식도 정리할 수 있다.
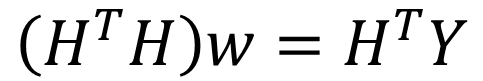

Another Approaches
· 선형 연립방정식을 푸는 것(SLE, Solving Linear Equations)은 선형 회귀를 푸는 가장 간단한 접근이다.
· 선형회귀를 푸는 다른 접근으로는 경사하강법(Gradient Descent Approach), 최대 우도 추정법(Maximum Likelihood Estimation Approach)가 있다.
'DataScience > 머신러닝' 카테고리의 다른 글
| 머신러닝 :: New Interpretation of Linear Regression(MLE) (0) | 2023.04.24 |
|---|---|
| 머신러닝 :: Model Optimization, Evaluation, Cross Validation (0) | 2023.03.21 |
| 머신러닝 :: k-NN for Classification, Regression (0) | 2023.03.20 |
| 머신러닝 :: 개요, 머신러닝 딥러닝 차이 (0) | 2023.03.20 |
| 머신러닝 :: 머신러닝 추천 서비스 구현_데이터 필터링, 쿼리셋 다루기 _TIL67 (1) | 2022.12.08 |




댓글