
머신러닝 :: 2. k-NN(k-Nearest Neighbors) for Regression, Classification
k-NN?
· 입력받은 Data x의 특성을 파악하기 위해, k개의 가장 가까운 Data들을 통해 특징을 추출해내는 지도학습 알고리즘
· k-NN은 Data labeling이 되어있어 지도학습에 속한다. 여기서 학습(training)은 '데이터를 저장하는 단계', 테스트(test)는 '거리 계산 단계' 로 볼 수 있다.
k-NN의 특징
· Case-based reasoning (instance-based, memory-based) : 찾고자 하는 값과 같은 값이 있으면 즉시 답하고, 없으면 가까운 값으로 답한다.
· Lazy learning : 러닝타임 동안에는 하는 것이 없다.
*Lazy : wait for query before generalizing ↔ Eager : generalize before seeing query
· Non-parametric method : Model을 찾지 않음 → 몇 개의 data를 쓰는지에 따라 결과가 달라진다.
*parametric : 선형 회귀의 경우와 같이 data를 대표할 수 있는 model을 찾으며, 모델에 따라 data에 근사시키는 값이 달라진다.
· 양의 정수 k값은 Hyperparameter로써 적절한 값을 직접 정해주어야 한다.
· Continuous Data는 크다/작다를 판단 가능하지만, Categorical Data는 축을 어디에 두느냐에 따라 결정경계가 달라진다.
· k-NN의 장/단점
| 장점 | 단점 |
| - Data 및 정보(information) 손실이 없다. | 모든 거리를 계산해야 하기 때문에 Test Time이 너무 오래 걸린다. |
| - 이해하기 쉬움 | Training Data의 지역적(local) 구조에 영향을 받으며, 불균일하면 결과에 영향을 준다. (ex. Major class가 많을 경우) |
| No training (Only inference step) | 모든 데이터를 사용하기 때문에 저장 공간이 필요하다. |
| Complexity of target functions do not matter | 노이즈에 민감하다 |
| 고차원 공간에서는 실제로 최근접 이웃이 nearest라고 볼 수 없는 경우가 발생(Curse of dimensionality) → 거리가 먼데 nearest인가? |
분류(Classification with k-NN)

· 분류(Classification) = Class = Category = Label = Tag
· k값이 작을 수록 결정경계가 민감(=sensitive)하고, k값이 커질 수록 결정경계는 관대(=generative)해진다.

회귀(Regression with k-NN)

· 출력값이 실수(Floating number)로 나올 경우 회귀(Regression)가 사용된다.
· x로부터 가까운 x_k들의 출력값 y_k의 평균값을 y로 한다.
· k값이 작을 수록 결정경계가 sensitive하고, k값이 커질 수록 결정경계는 generative해진다.
: small k → Higher Variance(less stable), large k → higher bias(less precise)
· 데이터에 따라 적절한 k 선택이 필요하며, 적절한 k값을 찾기 위해 Cross-validation을 사용할 수 있다.

k-NN 변형(Variation of k-NN)
· 단지 갯수를 세거나 평균값을 계산하는 것 뿐 아니라, 거리(Distance)에 대한 가중치(Weight)를 부여할 수 있다.
· k-NN 분류(Classification)의 변형

· k-NN 회귀(Regression)의 변형
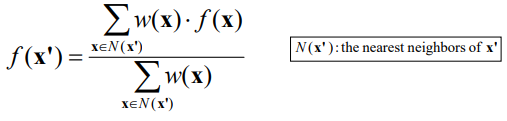
· 거리에 대한 가중치는 아래와 같다.

· 하지만 위 식은 거리가 매우 가까울 경우 무한대(Infinite)로 발산하는 문제가 있다. 이를 보완하기 위해 가중치에 대한 식을 아래와 같이 두 개의 식으로 변환하여 사용하면 Distance가 0에 가까울 경우 너무 큰 가중치 값에 따른 문제를 보완할 수 있다.

Kernel Regression
· 위 2가지 보완식 중 첫번째는 Kernel Regression으로, 더 가까이 있는 정도를 Kernel 함수(Gaussian Weight Function)를 통해서 Weight로 하여 계산을 한다.

· 가중치에 대한 식을 잘 보면 자연상수 e의 지수로 거리(Distance)와 람다(λ)가 있다. 람다(λ)값이 커질 수록 거리(Distance)의 영향은 줄어들기 때문에 아래 그림과 같이 경계가 더 관대(=generous)해진다.

Distance Measure
· Kernel Regression을 사용할 때 거리에 대한 정의가 중요하다. 예를 들어 아래 그림처럼 Data가 위치하고 있는 차원의 scale을 조정하면 Detail이 변화되어 경계의 구분이 어려웠던 부분이 명확히 구분되기도 한다.

· 거리를 표현하는 방법은 아래와 같이 여러가지가 있다.
: Generalized Euclidean distance, Mahalanobis distance, Cosine similarity, Pearson correlation, Jaccard similarity
*여기서 Similarity가 거리로 표현되는 것이 의아할 수 있는데, Similarity와 Distance는 역의 관계이다. 즉, Similarity를 정의할 수 있으면 Distance를 정의할 수 있다.
· kNN은 거리만 잘 정의할 수 있다면 위와 같은 도구들로써 수치형(Numerical) 데이터 뿐 아니라 Norminal, Categorical data(including sets, text, etc...)도 사용 가능하며, Euclidean 거리 뿐 아니라 다른 거리들도 사용가능하다.
· 자주 사용되는 Generalized Euclidean distance로는 아래와 같다.
1) L_1 norm(Manhattan distance) :

2) L_2 norm(Eucidean distance) :
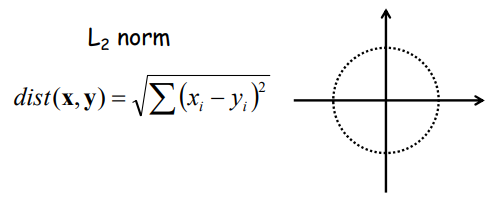
3) L_k norm :
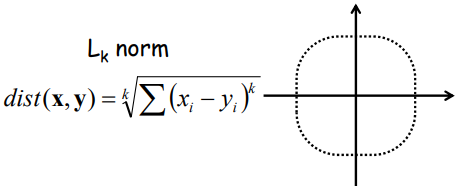
4) L_infinity norm :

· Mahalanobis distance : 정규화된 공간에 위치시킨 유클리디안 거리
1) Un-correlated case : 거리의 제곱를 분산(σ²)만큼 나누어준다.


2) Correlated case : 거리 계산에 공분산(Covariance)을 적용한다.


· Cosine Similarity : 거리의 크기보다 요소의 비율이 더 중요한 경우에 사용한다.
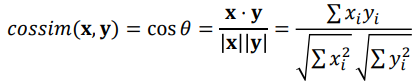

· Pearson Correlation Coefficient : 거리의 크기보다 각 차원간의 상관성이 더 중요한 경우에 사용한다.
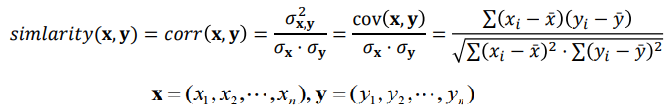
상관관계가 커질수록 유사도의 절대값은 0에서 1에 가까워진다. 즉, 상관성이 거의 없으면 0으로 수렴하고, 양의 상관관계가 있으면 양의 정수 1로, 음의 상관관계가 있으면 음의 정수 -1로 수렴하게 된다.

· 위의 두 경우(Cosine Similarity,Pearson Correlation Coefficient)에서 아래 케이스는 어떻게 바라볼 수 있는가?
| 예를들어, 콜라를 2번, 사이다를 3번 마신 사람과 콜라를 4번, 사이다를 6번 마신 사람은 유사한가? 또는, 콜라를 1번, 사이다를 2번 마신 사람과 콜라를 5번, 사이다를 5번 마신 사람은 유사한가? |
· Jaccard Similarity : 집합 관계를 사용하여 유사도를 측정하는 방법이다.
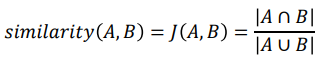
Reducing Computational Cost
· k-NN을 사용하는 것은 시간 복잡도 측면에서 비효율적이다. O(nd)
· 방법 1) 공간 구분 : Quad-tree, Locality sensitive hashing, etc...
· 방법 2) 전처리 : 차원 축소(덜 중요한 feature 제거, 벡터 양자화Vector Quantization), Data 사이즈 축소(Sampling, Clustering)
'DataScience > 머신러닝' 카테고리의 다른 글
| 머신러닝 :: Model Optimization, Evaluation, Cross Validation (0) | 2023.03.21 |
|---|---|
| 머신러닝 :: Linear Regression(선형 회귀식 풀이법, SLE) (0) | 2023.03.20 |
| 머신러닝 :: 개요, 머신러닝 딥러닝 차이 (0) | 2023.03.20 |
| 머신러닝 :: 머신러닝 추천 서비스 구현_데이터 필터링, 쿼리셋 다루기 _TIL67 (1) | 2022.12.08 |
| Web 개발 :: 프로젝트 조회수, Permission, Dataframe, 머신러닝_TIL66 (0) | 2022.12.07 |




댓글