
통계학_확률, 베이즈 정리
사상 & 표본공간
- 확률실험 (random experiment) : 확실히 예측할 수 없는 결과를 유발하는 행위 또는 과정
- 표본공간 (sample space) : 출현가능한 모든 단일사상들의 집합
- 사상 (events) : 표본공간의 부분집합, 하나 이상의 단일사상의 집합
- 근원사상 (elementary outcome, =단일사상) : 표본공간을 구성하는 분해할 수 없는 무작위 실험의 기본적인 결과
- 여사상 (complement) : 특정 사상의 나머지 집합, P(A^c) = 1-P(A)
확률(Probability)
- 각 근원사상들이 발생할 가능성이 발생할 가능성이 같을 때, 사상 A의 확률 P(A)는

확률의 성질
- 임의의 사상 A에 대하여
1) 0 ≤ P(A) ≤ 1
2) P(S) = 1
3) 서로 배반인 사상열 A_i, i=1, 2, ... 에 대하여
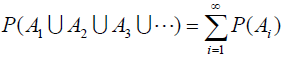
조건부 확률(Conditional probability)
- 사상 A에 관한 정보가 주어졌을 때, B가 발생할 확률
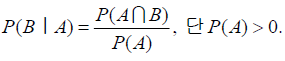
독립(Independent)
- 표본공간에서 정의되는 두 사상 A와 B의 발생이 서로 무관하여 영향을 주지 않는 경우
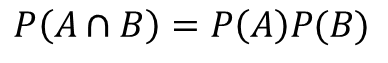
- 두 사상 A, B가 독립이기 위한 필요충분조건
1) P(A|B) = P(A), P(B) > 0
2) P(B|A) = P(B), P(A) > 0
3) P(AB) = P(A)P(B)
- n개의 사상 A1, ..., An이 상호독립이기 위한 필요충분조건
: P(A1∩...∩An)=P(A1)...P(An)
종속(Dependent)
- 두 사상 A와 B의 발생이 서로 영향을 받는 경우
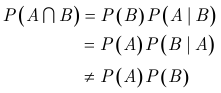
확률의 합법칙

확률의 곱법칙

분할
- 사상 A1, A2, ..., An이 표본공간 S에 대하여 다음 조건을 만족할 경우, S에 대한 분할이라고 한다.
1) Ai∩Aj = Φ, (단, i ≠ j)
2) ∪Ai = s *모든 사상 Ai(i = 1, ..., n)의 합
전확률(Total Probability)의 정리
- 상호배반사상인 B1, ... ,Bn이 표본공간 S를 분할할 경우, 임의의 사상 A에 대해 다음이 성립
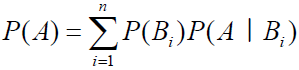
베이즈 정리
- 상호배반사상인 B1, ..., Bn이 표본공간 S를 분할할 경우, 모든 i에 대해 P(Bi)>0이라 하면, P(A)>0인 사상 A에 대하여 다음의 식이 성립한다.
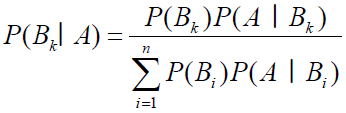
'DataScience > 통계학' 카테고리의 다른 글
| 통계학 _ 기대값, 분산, 체비셰프의 부등식, 적률 (0) | 2023.07.15 |
|---|---|
| 통계학 _ 이산형 확률변수, 연속형 확률변수 (0) | 2023.07.14 |
| 통계학 _ 기술 통계학 (0) | 2023.07.12 |
| 통계학 _ 통계 기본 개념(모집단, 모수, 표본, 통계량) (0) | 2023.07.03 |




댓글