
통계학_기대값, 분산, 체비셰프의 부등식, 적률
기대값(Expected value)
- 사건이 발생했을 때, 이득과 그 사건이 발생할 확률을 곱한 값을 전체 사건에 대하여 합한 값
(=어떤 확률적 사건에 대한 평균의 의미를 가진다.)

분산(Variance)
- 확렬변수가 기대값으로부터 얼마나 떨어진 곳에 분포하는지 나타내는
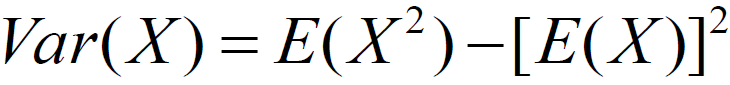
기대값과 분산의 성질
Let X ~(μ, σ²), c: 상수
1) E(c) = c
2) E(X) = μ
3) E(cX) = cE(X) = cμ
4) V(c) = 0
5) V(X) = σ²
6) V(c, X) = c²V(X) = c²σ²
7) E(X₁+X₂) = E(X₁) + E(X₂) = μ₁+μ₂
8) V(X₁+X₂) = V(X₁) + V(X₂) + 2Cov(X₁+X₂)
*Cov(X₁+X₂) = E(X₁-μ₁)(X₂-μ₂)
Cov(Covariance, 공분산) : 두 변수가 같은 방향으로 가려는 경향(양의 상관관계, 음의 상관관계 → 상관계수)
9) V(X₁-X₂) = V(X₁) + V(X₂) - 2Cov(X₁+X₂)
10) X₁, X₂가 독립일 경우, V(X₁±X₂) = V(X₁) + V(X₂)
11) E(X₁·X₂) = E(X₁) · E(X₂)
12) E(X₁ ÷ X₂) ≠ E(X₁) ÷ E(X₂)
확률변수의 함수의 분산
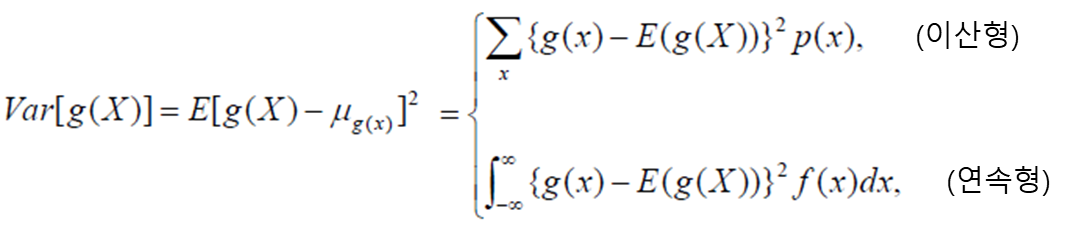
마르코프 부등식(Markov Inequality)
- 확률변수 X에 대해서 임의의 함수 U(X)≥0과 임의의 모든 양의 상수 c에 대해서 아래 식이 성립한다.
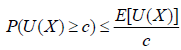

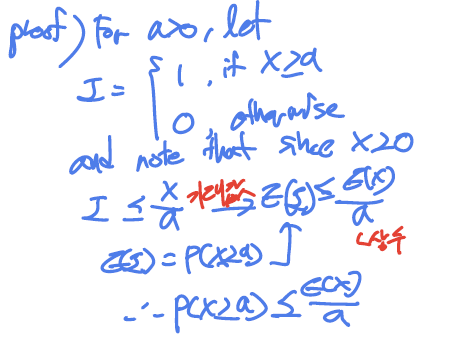
체비셰프 부등식(Chebyshev Inequality)
- 확률변수 X의 평균과 분산이 각각 μ와 σ²일 때(단, μ<∞, σ²<∞), k>0인 상수에 대해 다음의 부등식이 성립한다.
*정규분포를 따르지 않는, 왜도가 있는 분포에서는 체비셰프의 부등식을 이용하여 확률을 구할 수 있다.

적률과 적률생성함수
- 적률(Moment) : 확률변수(또는 분포)의 적률은 확률분포를 가지는 확률변수의 거듭제곱의 기대값을 말한다
- X를 기대값이 존재하는 확률변수라 할 때, X의 r차 적률은 아래와 같다.


- 중심적률(central moment) : 확률변수 X가 있을 때, a에 대한 X의 r차 중심적률은 E[(X-a)^r]으로 정의한다. 만약 a=μ_X라면 μ_X에 대한 X의 r차 중심적률은 μ_r로 표현하고 다음과 같다.

- 분위수(Quantile) : 확률변수 X의 확률분포의 q번째 분위수 ξ_q는 F_X(ξ) ≥ q를 만족하는 가장 작은 ξ값
- 중앙값(Median) : 확률변수 X의 확률분포의 중앙값은 50분위수를 말한다. (ex. med_x ,med(X), ξ_0.5)
- 계승적률(Factorialmoment) : E[X(X-1)···(X-r-1)]
- 적률생성함수 : 확률변수 X에 대한 확률밀도함수 f(x) 또는 확률질량함수 p(x)에서 임의의 구간 -h < t < h에서 모든 t에 대해 기대값이 존재한다면 e^tx의 기대값을 X의 적률생성함수라 하며 아래와 같이 표현할 수 있다.
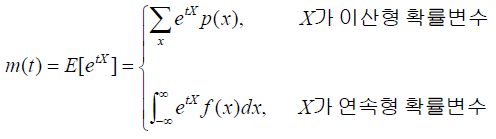
- 확률변수 X의 기대값이 존재한다면 E(t^x)를 계승적률생성함수(Factorial moment generating function)라고 한다.
'DataScience > 통계학' 카테고리의 다른 글
| 통계학 _ 이산형 확률변수, 연속형 확률변수 (0) | 2023.07.14 |
|---|---|
| 통계학 _ 확률, 베이즈 정리 (0) | 2023.07.13 |
| 통계학 _ 기술 통계학 (0) | 2023.07.12 |
| 통계학 _ 통계 기본 개념(모집단, 모수, 표본, 통계량) (0) | 2023.07.03 |




댓글