
통계학_이산형 확률변수, 연속형 확률변수
확률 변수(Random Variable)
- 확률적 시행의 결과에 따라 결과 값이 결정되는 변수
- 이산형(Discrete) 확률변수
→ 이산형 확률분포, 확률질량함수(Probability Mass Function, Pmf)
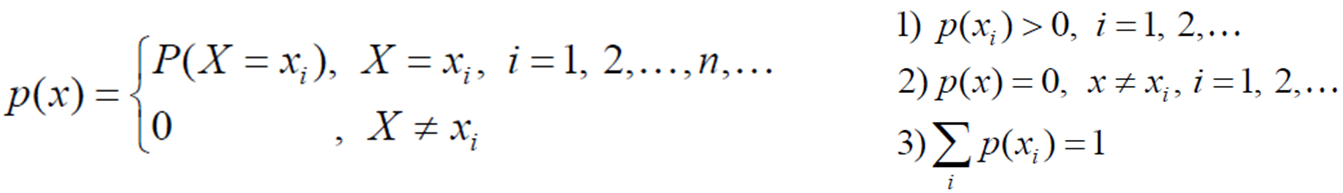
→ 이산형 확률변수의 누적분포함수

* 특성
1) F(∞) = 1, F(-∞) = 0
2) F(x)는 단조함수이면서 비감소함수이다. F(a) ≤ F(b) (*단 a < b)
3) F(x)는 h가 0으로 변화하는 구간에서 연속이다. lim F(x+h) = F(x) (*
- 연속형(Continuous) 확률변수
→ 연속형 확률분포, 확률밀도함수(Probability Density Function, Pdf)

→ 연속형 확률분포에서 X가 a와 b사이의 값을 취할 확률 (*아래 식에서 보듯 등호는 의미가 없다)
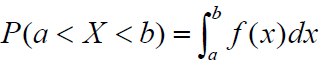
→ 연속확률분포에서 한 점에서의 확률은 0이다.
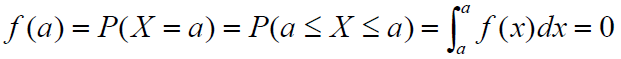
→ 연속형 확률변수의 누적분포함수

* 특성
1) P(a < X < b) = F(b) - F(a)
2) f(x) = dF(x) / dx
반응형
'DataScience > 통계학' 카테고리의 다른 글
| 통계학 _ 기대값, 분산, 체비셰프의 부등식, 적률 (0) | 2023.07.15 |
|---|---|
| 통계학 _ 확률, 베이즈 정리 (0) | 2023.07.13 |
| 통계학 _ 기술 통계학 (0) | 2023.07.12 |
| 통계학 _ 통계 기본 개념(모집단, 모수, 표본, 통계량) (0) | 2023.07.03 |




댓글