
통계학_기술통계
자료의 분류
(1) 범주형 자료(Categorical data)
: 숫자로 표현이 불가한 자료를 집단화하여 나타낸 자료(질적자료: 명목형, 순서형)
(2) 측정형 자료(Measurement data)
: 각 관측대상이 되는 자료에 측정단위에 따른 측정값을 부여하여 얻어진 데이터로 숫자의 크기에 의미가 있는 자료(양적자료: 이산형, 연속형)
척도에 대한 분류
(1) 명목척도(Norminal) : 빈도 분석
(2) 순서척도(Ordinal) : 차례가 있으며 각 간격은 다를 수 있다..(ex. 초, 중, 고)
(3) 구간(=등간)척도(Interval) : 간격과 순서가 있는 척도
(4) 비율척도(Ratio) : 절대 0점이 있는 척도(연산이 가능)

위치의 측도
*통계학의 3M : Mean(평균), Median(중앙값), Mode(최빈값)
- 평균(Mean) : 자료의 합을 자료의 수로 나눈 값, 자료의 Outlier에 Robust하지 않다.
- 모평균

- 표본평균

- 중앙값(Median) : 자료를 크기 순으로 나열했을 때 중앙에 위치한 값

- 최빈값(Mode) : 가장 발생빈도가 높은 관찰값
*최빈값은 같은 값을 가진 데이터가 없는 경우 존재하지 않을 수도 있다.
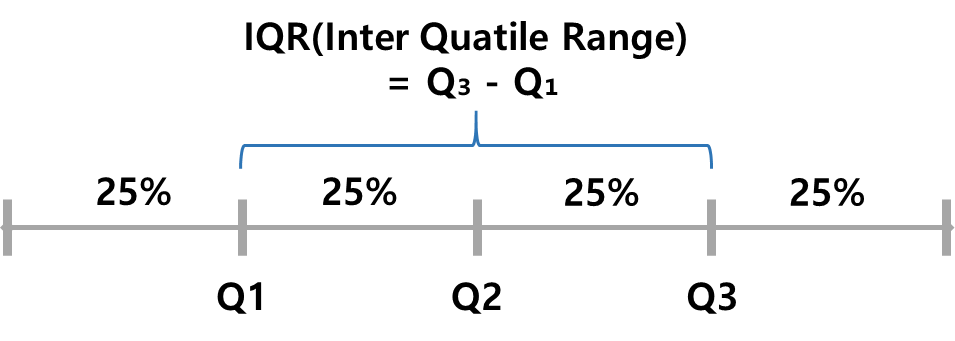
- 백분위수 : 크기 순으로 배열한 자료를 100등분하는 수로 제100p백분위수란(0 ≤ p ≤ 1) 자료를 크기 순으로 배열하였을때 100p%의 관찰값이 그 값보다 작거나 같고 100(1-p)%의 관찰값이 그 값보다 크거나 같게 되는 값
- 사분위수 : 자료를 크기 순으로 배열하였을 때 전체 관찰값을 4등분하는 위치에 있는 값
분산과 표준편차
- 분산 : 자료의 변동(Variation, 관찰값과 평균값의 차에 제곱한 값)의 평균
- 표준편차 : 분산의 양의 제곱근
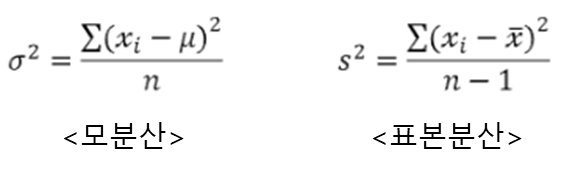
- "편차"의 합은 0이기 때문에 모분산에서는 "편차 제곱"의 합을 이용한다.
- 산포를 보기 위해 분산을 만들었는데 왜 표준편차를 확인해야 하는가?
: 평균들은 1차식(1차원)이지만 분산은 2차식(2차원)으로 같은 선 상에서 비교하기 어렵기 때문이다.
* 평균(1차식) → 1차 적률
* 분산(2차식) → 2차 적률
* 왜도(3차식) → 3차 적률
* 첨도(4차식) → 4차 적률
- 모집단은 n으로 나누는데 표본분산은 n-1로 나누는 이유?
1) 표본 분산의 자유도(DOFs)가 n-1이기 때문
2) 표본 분산은 모집단의 분산에 비해 크기가 작아 underestimatied될 수 있어 이를 보정(Unbiased estimate)
(*참고 : [출처] 왜 표본(샘플)의 분산에서는 n이 아닌 n-1로 나눌까?|작성자 PN _ 링크)
- 표본분산의 식 간소
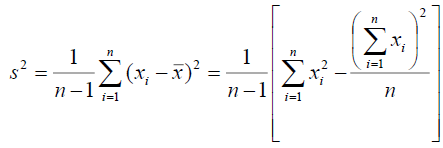
변동계수
- 평균과 표준편차를 동시에 고려한 상대적 변동
- 표본 변동 계수
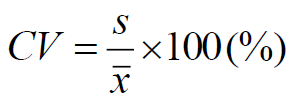
- 왜도(skewness) 계수

- 첨도(Kurtosis) 계수

'DataScience > 통계학' 카테고리의 다른 글
| 통계학 _ 기대값, 분산, 체비셰프의 부등식, 적률 (0) | 2023.07.15 |
|---|---|
| 통계학 _ 이산형 확률변수, 연속형 확률변수 (0) | 2023.07.14 |
| 통계학 _ 확률, 베이즈 정리 (0) | 2023.07.13 |
| 통계학 _ 통계 기본 개념(모집단, 모수, 표본, 통계량) (0) | 2023.07.03 |




댓글